NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres		DicoNombre NOMBRES										Glossaire Nombres
1 10 100 500 1000 1500 1900		2 000 à 2 999										3000 / 5000 10 000 20 000 50 000 100 000 10^6 10^9 10^100
2 000 à 2 999				Maths			Dates			Jeux
2 000	2 100		2 200		2 300	2 400	2 500	2 600	2 700		2 800		2 900

2 500

Multimédia	· 2 500 caractères dans une page d'un livre  Typiquement: 40 lignes de 60 caractères	>>>
Histoire	· 2538-2516 av. J.-C. Pharaon Kheops	Pyramide
Biologie	Dépense moyenne de santé en 2002 · 2 579 euros pour chaque Français. · 158 milliards d'euros total France. Ces dépenses pèsent pour 10 % du PIB.

Propriété générale: La somme des impairs jusqu'à n est égale à

la demi-somme des extrêmes au carré: (1 + n)² / 4.

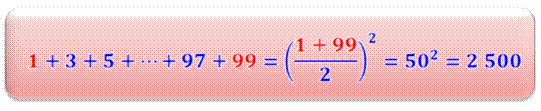
2 500 = 50²	· Base du calcul mental des carrés des nombres voisins de 50.
2 500 = 500²	· Opération avec ses chiffres.
2 500 = 5^5 – 5^4	· Différence de puissances de 5.
2 500 = 1 + 3 + 5 + … + 99 = 50² et 99 = 2 x 50 – 1	· Somme des impairs consécutifs jusqu'à 100. Propriété de tous les carrés.
2 500 = 50² & 22 500 = 150² & 62 500 = 250²	· Reste carré deux fois en lui ajoutant un chiffre à gauche.
–2 500 = (5 + 5i)^4 = (5 – 5i)^4	· Entier = puissance de nombre complexe.

2 501 = 51² – 10² = 61 x 41

= 50, 009999000199950014…²

· Différence de carrés.

· L'écart devient inférieur au 1/100 entre racines voisines.

2 510

· Nombre de Mian-Chowla.

2 519 = PPCM (2, 3, 4, 5, 6, 7, 8, 9, 10) – 1

· Application au défilé de New-York.

2 519	= 2 × 1 259	+ 1
	= 3 × 839	+ 2
	= 4 × 629	+ 3
	= 5 × 503	+ 4
	= 6 × 419	+ 5
	= 7 × 359	+ 6
	= 8 × 314	+ 7
	= 9 × 279	+ 8
	= 10 × 251	+ 9

· Nombre qui a pour restes les nombres successifs de 1 à 9 lorsque divisé par les nombres successifs de 2 à10.

· Avec 2518, les restes vont de 0 à 8.

· Avec 2520, les rests sont nuls

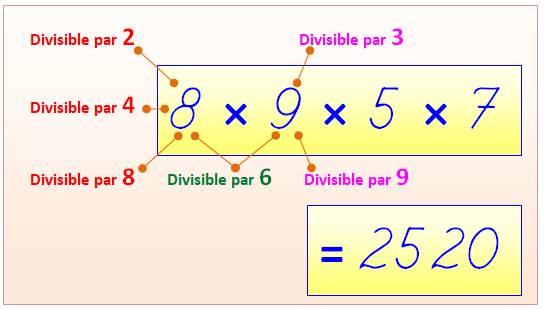
Plus petit nombre divisible par {1 à 10}

2 520 = 2^3 × 3^2 × 5 × 7 = 3 × 4 × 5 × 6 x 7 = 5 × 7 × 8 × 9 est divisible par 1, 2, 3, 4, 5, 6, 7, 8, 9 et 10 = 8! / 4² = 8! / (2 × 2!)² = 8! / 2^4 = 9! / 12² = 9! / (2 × 3!)² = (2+2+2+2)! / (2!×2!×2!×2!)		· Hautement composé: 48 diviseurs. · Le plus petit nombre divisible par les nombres de 1 à 10. · PPCM des nombres de 1 à 9 et aussi, des nombres de 1 à 10. · Factorielle tronquée. · Super-primorielle de 9 et de 10. · Nombre Multi Pronique · Voir 2 519 ci-dessus · Factorielles divisées
	· Pour trouver le nombre divisible par tous les nombres de 1 à 10: Sélectionner chacun des nombres premiers (2, 3, 5 et 7), et Conserver la plus grande puissance de chacun.
252, 280, 315, 360, 420, 504, 630, 840, 1260, 2520	· Chaine harmonique La sixième la plus longue.
2 520 = 120 x 21 = 210 x 12	· Nombre EPRN, le plus petit.

Voir Brève 54-1072

Illustration

Voir Brève 24-467

2 521	· Nombre étoilé.
2 522 = 2 × 13 × 97 2 523 = 3 × 29^2 2 524 = 2^2 × 631 2 525 = 5^2 × 101 2 526 = 2 × 3 × 421 2 527 = 7 × 19^2 2 528 = 2^5 × 79 2 529 = 3^2 × 281	· Six nombres consécutifs comportant trois facteurs. Plus petit cas.
	· Le cumul de la somme des inverses des diviseurs des nombres jusqu'à 2 525 passe le seuil du nombre entier 6.
2 538² = 6441444	· Carré avec chiffre 4 répété.
2 530 = 3^7 + 7^3 = 2187 + 343	· Nombre de Leyland.
2 540^1/2 = 50,39841267…	· Les dix premiers chiffres sont pannumériques.
25 50 = 2 + 4 + 6 + … + 100 = 50 x 51 250 500 = 2 + 4 + …+ 1000 = 500 x 501 2500 500 = 2 + 4 + …+ 10 000 = 5000 x 5001	· Somme des pairs jusqu'à 100. Motifs semblables pout les autres puissances de 10. · Somme des pairs jusqu'à 2n = n (n + 1)
2 556 = 1^3 + 3^3 + 5^3 + 7^3 + 9^3 + 11^3	· Somme des six premiers impairs au cube.
2 560 = 2^9 . 5 & 2 × 5 = 9 + 1	· Produit des facteurs égal somme des exposants.
1+1+2+3+5+8+13+21+34+ 55+89+144+233+377+610+987 = 2 583 = 21 x 123	· La somme de 16 nombres de Fibonacci consécutif est divisible par 21.
987, 1 597, 2 584, 4 181, 6 765	· Nombre de Fibonacci (n°18).
2 586	· Quantité d'additions distinctes avec quatre termes de 0 à 100.

2 592 = 2^5 x 3^4	· Nombres et puissances consécutives. Ce nombre possède 30 diviseurs. · Nombre d’Achille fort.
2 592 = 2^5 . 9^2 = 32 x 81	· Nombre dit faute de frappe (printer's errors). · Seul motif de ce type à 4 chiffres (Dudeney) Suivant (pseudo) à 5 chiffres: 3^4x 425 = 34 425 = 81 x 425 Trouvé par D. L. Vanderpool. Suivant (tronqué) à 6 chiffres: 117 649 = 1^1 x 7^6. · Seul nombre qui est sa propre transformation powertrain.
2 592 = phi(5 186) = phi(5 187) = phi(5 188)	· Cas unique connu pour le totient.
	· Deux fois sommes de trois cubes, plus petite configuration découverte par Ramanujan.

2 600

2 606 = 24² + 25² + 26² + 27² = 4 x 25 x 26 + 6

· Exemple pour un tour de magie: retrouver les quatre nombres consécutifs en ne connaissant que la somme de leur carré.

Facteurs	2 620 = 1 . 2² . 5 . 131
Diviseurs	1, 2, 4, 5, 10, 20, 131, 262, 524, 655, 1310, 2620
Quantité	12
Somme	5 544
S – N	2 924

· La paire 2 620 et 2 924 est amiable.

2 625 = 3 x 5³ x 7

· Nombre formé de deux nombres consécutifs concaténés et produit de premiers successifs.

2 636² = 6948496

· Carré palindrome d'un nombre non-palindrome.

· Factorielle septuple de 3
= (7x0+1) (7x1+1) (7x2+1) (7x3+1)
= 1 x 8 x 15 x 22

2 664 = (100 – 26) (100 – 64)

= 74 x 36

· Nombre complémenté à 100.

2 664 = 345 + 354 + … + 543

= 222 (3 + 4 + 5)

· Somme des permutations des nombres formés des trois chiffres 3, 4 et 5.

Géographie

· 2 685 km point Nemo  Point de la planète situé au milieu de l'océan pacifique; il est le plus éloigné de toutes les terres.

>>>

2 700

2 704 = 52² et 4(2+7+0+4) = 52 5 184 = 72² et 4(5+1+8+4) = 72 7 744 = 88² et 4(7+7+4+4) = 88	· Nombres dont la somme des chiffres est quatre fois sa racine carrée.
2 730 = 2 x 3 x 5 x 7 x 13	· Produit de nombres premiers successifs.
273010 = 1010101010102 = 2^11 + 2^9 + 2^7 + 2^5 + 2^3 + 2^1 273010 = 22222224 = 2 (4^5 + 4^4 + 4^3 + 4^2 + 4^1 + 4^0) 2730 = 2/3 (4^6 – 1) = 2/3 x 4 095 = 2 x 1 365		· Répétition de 10 en binaire. Somme des premières puissances impaires de 2. · Repdigit en base 4. Double de la somme des premières puissances de 4.
2 730 divise n^13 – n	· Divisibilité
88² + 33² = 8833	· Les chiffres des deux nombres se retrouvent dans la somme de leurs carrés. Un exemple avec chiffres dans l'ordre.
2 772 = 12 x 231 = 21 x 132	· Nombre palindrome doublement divisible par des retournés.
2 772 = 2 x 7 x 198	· Plus petit nombre en 2 et 7, divisible par 2 et 7.
2 773	· Nombre étoilé.
2 773 = 2²+7²+7²+3² + 7^3+6^3+8^3+9^3+5^3+2^3+9^3 2773^2 = 7 689 529	· Narcissique de Keith · Somme des carrés des chiffres et des chiffres au cube de son carré.
2 780	· Nombre de Mian-Chowla.
2 791 = 2²+7²+9²+1² + 7^3+7^3+8^3+9^3+6^3+8^3+1^3 2791^2 = 7 789 681	· Narcissique de Keith. Le plus grand à deux termes Somme des carrés des chiffres et des chiffres au cube de son carré.

2 900

2 916 = 54² et 3(2+9+1+6) = 54

· Seul nombre dont la somme des chiffres est trois fois sa racine carrée.

Suite	· Nombres 2800 à 2999
Voir	· Nombre Chanceux · Semaine · Palindrome Triangle · Tectroèdre · Raisonnement · Rep Unit · Suites · Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N2500.htm