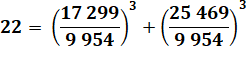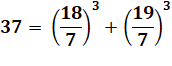|
Édition du: 13/11/2024 |
|
INDEX |
Nombres CUBES |
|||
|
Cubes
– Partition |
||||
|
Somme
= Carré |
Deux
cubes – Multi |
|||
![]()
|
SOMMES de DEUX CUBES n = x3 + y3 Sommes de
nombres entiers
au cube
et aussi sommes de rationnels
(fractions). Sans ordinateur, Dudeney avait trouvé des
solutions en nombres rationnels pour le nombre 9 et pour le nombre 17:
|
||
|
|
Sommaire de cette page >>> Sommes de deux cubes – Nombres entiers >>> Les défis de Dudeney >>> Identité de Fermat >>> Géométrie analytique >>> Sommes de deux cubes – Nombres rationnels |
Débutants Glossaire |
|
Les 42 nombres, somme de deux cubes
jusqu'à n = 1001 Lecture: 9 = 13
+ 23 = 1 + 8 ; 35 = 23 + 33 = 8 + 27.
Les 202 nombres, somme de deux
cubes jusqu'à n = 10 000 2, 9, 16, 28, 35, 54, 65, 72, 91, 126, 128, 133, 152,
189, 217, 224, 243, 250, 280, 341, 344, 351, 370, 407, 432, 468, 513, 520,
539, 559, 576, 637, 686, 728, 730, 737, 756, 793, 854, 855, 945, 1001, 1008,
1024, 1027, 1064, 1072, 1125, 1216, 1241, 1332, 1339, 1343, 1358, 1395, 1456,
1458, 1512, 1547, 1674, 1729, 1736, 1755, 1792, 1843, 1853, 1944, 2000, 2060,
2071, 2198, 2205, 2224, 2240, 2261, 2322, 2331, 2413, 2457, 2540, 2662, 2709,
2728, 2745, 2752, 2771, 2808, 2869, 2926, 2960, 3059, 3087, 3197, 3256, 3376,
3383, 3402, 3439, 3456, 3473, 3500, 3528, 3591, 3718, 3744, 3887, 3925, 4075,
4097, 4104, 4123, 4160, 4221, 4312, 4375, 4394, 4439, 4472, 4608, 4706, 4825,
4914, 4921, 4940, 4941, 4977, 5038, 5096, 5103, 5129, 5256, 5425, 5427, 5488,
5572, 5642, 5824, 5833, 5840, 5859, 5896, 5913, 5957, 6048, 6119, 6175, 6244,
6293, 6344, 6561, 6641, 6750, 6832, 6840, 6860, 6867, 6886, 6923, 6984, 7075,
7110, 7163, 7202, 7371, 7471, 7560, 7588, 7657, 7859, 8001, 8008, 8027, 8029,
8064, 8125, 8190, 8192, 8216, 8288, 8343, 8512, 8576, 8587, 8729, 9000, 9009,
9056, 9207, 9262, 9269, 9288, 9325, 9331, 9386, 9477, 9603, 9604, 9728, 9773,
9826, 9928, 9990. En autorisant les nombres négatifs,
toutes les solutions jusqu'à 100
|
|
|
Henry Ernest Dudeney (1857-1930) propose ces deux problèmes dans The Canterbury Puzzles and Other Curious
Problems. Sans ordinateur, on se demande comment il a pu
calculer ces valeurs. Voir Énigme des
trois maisons / Nombres
de Dudeney "It is hard nut, and should only be
attempted by those who flatter themselves that they possess strong
intellectual teeth". |
Puzzle du cube d'argent Il demande les dimensions de deux cubes d'argent
dont le volume total est 17 pouces-cube. Il faut trouver une paire de nombres rationnels
tels que la somme de leur cube soit 17.
Puzzle du Docteur en physique Il demande les rayons de deux sphères dont le
volume total est égal à celui de deux sphères de rayon 1 et 2 pouces. Il faut résoudre: x3 + y3 =
13 + 23 = 9
|
|
|
Méthodes Il existe au moins trois méthodes pour trouver de
telles sommes. |
1.
Recherche exhaustive par ordinateur
(ou par force brute); 2.
Utilisation de la géométrie
analytique: trouver un point rationnel sur une courbe; ou 3.
Partir d'une solution connue et trouver de nouvelles solutions à
l'aide d'identités |
|
![]()

Source: The Canterbury Puzzles and
Other Curious Problems (1908) – Pages 19
|
Fermat
propose une identité
qui permet de trouver une somme algébrique de deux cubes à partir d'une somme
connue. |
= a12
– 2a9b3 + 2a3b9 – b12 |
|
|
Exemple avec 9 = 23
+ 13 Le doublet (2, 1) permet de créer le doublet (20,
-17), avec nombre négatif. |
(a3 + b3)
(a3 – b3)3 = [2 · (23 + 2·13)
]3 – [1 · (2·23 + 13) ]3 9 · 73 = 203
– 173 Effectivement: 203 –
173 = 8 000 – 4 913 = 3087 = 9 · 73 Soit deux nouveaux cubes: 20 et 17. Autrement dit:
|
|
|
Nouvelles itérations Pour tenter de trouver une solution à deux nombres
positifs. |
Les calculs faits, on trouve cette nouvelle somme
pour 9:
|
|
|
Encore une Enfin positive ! Dudeney connaissait l'identité de Fermat et avait
trouvé ce résultat. |
|
|
|
Dudeney n'en est pas resté là, il voulait plus
petit. Sans doute à partir cette identité négative, il a
calculé la positive. |
|
|
|
L'idée consiste à représenter la courbe x3
+ y3 = 9, par exemple
(Tracé avec GeoGebra). Le point (x, y) = (1, 2) est connu. Les tangentes
à la courbe passant par ce point coupent la courbe en deux points. On vérifie que les coordonnées de ces points
répondent à l'identité: la somme de leurs cubes vaut 9. La suite du raisonnement fait appel aux
propriétés des courbes
elliptiques. Le mathématicien Eugenia Rosu
propose la formule:
Voir Articles spécialisés en référence |
|
|
|
Nombres somme de deux nombres
rationnels Chacun une infinité de fois. Sont exclus les cubes et deux fois les cubes. |
Liste des nombres somme de deux
cubes rationnels 6, 7, 9, 12, 13, 15, 17, 19, 20, 22, 26, 28, 30,
31, 33, 34, 35, 37, 42, 43, 48, 49, 50, 51, 53, 56, 58, 61, 62, 63, 65, 67, 68,
69, 70, 71, 72, 75, 78, 79, 84, 85, 86, 87, 89, 90, 91, 92, 94, 96, 97, 98,
103, 104, 105, 106, 107, 110, 114, 115, 117, 120, 123, 124, … |
||
|
Quelques exemples pour n jusqu'à
100
|
|
||
|
Quelques solutions explicitées Lecture
|
|||
Autres
solutions par Andy
Pepperdine
Merci
à Guy HEKIMIAN pour sa relecture attentive
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
|
||
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Partition/Som2Cube.htm
|
|