|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISION – AVANCÉ Comment effectuer
une division à deux
chiffres ou plus; norm Toutes les ét
On utilise plutôt l 16 / 3 et non 16 :
3 Remarquez que le reste (1) est toujours strictement inférieur au diviseur (3), sinon le quotient (5) devrait être augmenté. On se souvient que le quotient est le plus grand nombre de paquets de 3 que je peux extraire de 16. |
Retour à Initiation
|
En nombres entiers Exemple:
14 789 à diviser par 67 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
14 789 divisé par 67 = 220 et reste 49 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Résultat 14 789 / 67 = 220 avec 49
pour reste En effet 220 x 67 = 14 740
|
En résumé (disposition classique)
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
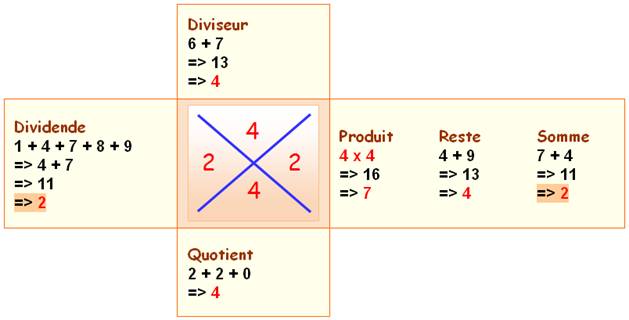
Preuve
par neuf
Voir Rappel du principe |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Notez la curiosité avec l'avant-dernier reste en 111… Voir Multiplications pannumériques |
|
|
But Comment programmer une division sans avoir
l'instruction division à disposition ? |
Une division est en fait une
succession de soustractions |
|
|
Programmation par boucles (Maple) Les
deux nombres sont a à diviser par b. Il
faut réaliser un maximum de soustractions de b dans a. Le
reste r est initialisé à a et le quotient à 0. Une
boucle est exécutée "tant que (while) le reste r est supérieur ou égal à
b. Alors
r est décrémenté de b et on compte une soustraction en plus (plus 1 sur q). Lorsque
la limite est atteinte, impression du quotient et du reste. |
|
|
|
Programmation par méthode récursive (Maple) Une fonction (ici nommée procédure) est
définie: elle exécute une soustraction. Le principe consiste à faire appel à la fonction
elle-même pour effectuer toutes les soustractions à la file. Chaque soustraction est exécutée tandis que
le nombre a décroit progressivement. En fin de récursion, impression du
quotient. Le reste n'est pas indiqué. Version Python L'exécution de ce programme
Python donne:
|
|
|
Voir Algorithmes et programmation de la division / Programmation – Index
/ Récursivité
![]()
|
Suite |
|
|
Retour Voir résumé en Très utile |
|
|
Voir |
|
|
Cette page |