|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉNOMBREMENTS
et DÉS Rappel: PROPRIÉTÉS des DÉS
|
Voir Initiation au dénombrement et aux
probabilités avec les dés
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple Avec 3 dés, il y a 15 possibilités d'avoir exactement deux fois le 6 sur un total de 216 possibilités avec ces
dés. Soit un ratio (une probabilité) de 15 / 216
= 6,9% Tableau
Voir Combinaisons
Cnp
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||
|
Lancer de |
Calcul |
Nombre de cas possibles |
Illustration |
|||||
|
1 dé |
|
6 |
a = {1, 2, … 6} => 6 |
|||||
|
2 dés |
|
6 x 6 = 62 |
a = {1, 2, … 6} => 6 b = {1, 2, … 6} => 6 |
|||||
|
n dés |
|
6n |
|
|||||
|
||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
Calcul méthode 1
Calcul méthode 2 - Exemple avec
3 dés
Voir Nombre 91 |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||
|
Calcul - Exemple avec 3 dés
Note:
on aurait pu compter de la manière suivante: configuration 66a avec a de 1 à
6 soit 6 cas; configuration 6a6 avec a de 1 à 6 soit 6 cas; configuration a66
avec a de 1 à 6 soit 6 cas. Le total donne
6 + 6 + 6 = 18 cas et non 16 ! Explication:
autant on distingue l'arrivée des 6 dans a66, 6a6 et 66a; autant on ne peut
distinguer un ordre d'arrivée pour 666. Cette configuration ne compte que
pour 1. Or, dans notre dernier calcul, il est compté à tord pour 3. |
|||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
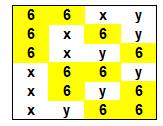
Généralisation à strictement 2 fois la valeur 6
Mais x
et y peuvent être intervertis, ce qui conduit à deux fois le compte. Non, car
lorsque x et y balaient les valeurs de 1 à 6, on retrouve les positions
symétriques: (1,5) et (5,1), par exemple. De ce fait, les inversions sont
déjà comptées. |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
Généralisation à strictement 3 fois la valeur 6
|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Se familiariser avec le cas de "au moins trois
fois le 6" pour 5 dés
Généralisation k fois le 6 pour n dés
Exemple au moins 5 fois le 6 pour 7 dés
Exemple au moins 5 fois le 6 pour 10 dés
|
|||||||||||||||||||||||||||||||||||||||||||||||||||

![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()