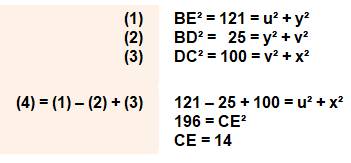|
Édition du: 04/08/2023 |
|
INDEX |
Quadrilatères |
||
|
Quadrilatère
– Introduction |
Quadrilatère
– Aire |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Résolution du quadrilatère orthodiagonal Un quadrilatère orthogonal
(diagonales perpendiculaires). Trois côtés sont
connus. Retrouver la longueur du quatrième côté et des diagonales. |
||
|
|
Sommaire de cette page >>> Quadrilatère orthodiagonal |
Débutants Glossaire |
Un
quadrilatère orthodiagonal particulier (aire = 100)
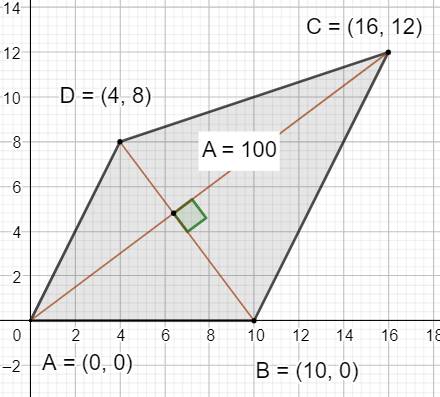
Voir Dissection du quadrilatère
|
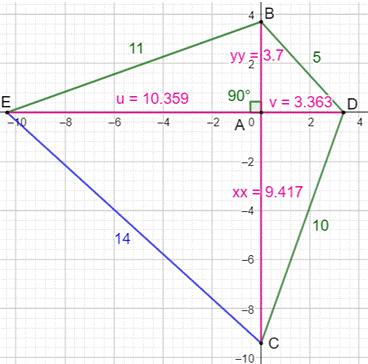
Question Soit ce quadrilatère orthodiagonal dont trois
côtés sont connus (en vert). Trouver la longueur du quatrième. Réponse Dans un tel quadrilatère les deux sommes des
carrés des côtés opposés sont égales. Démonstration
|
EB² + DC² = CE² + BD² = u² + y² + v² + x² |
|
|
Longueurs des fractions de
diagonales On compare l'aire calculée avec:
On dispose de quatre équations pour quatre inconnues.
C'est bien! Mais la résolution est assez délicate. En exprimant toutes les variables en fonction de
u²: Il faut alors résoudre cette équation avec des
radicaux:
|
Calculs des longueurs sur les
diagonales
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |