|
||||||||||||||||||||||||||||||||||||||||||||||||||
Niveau terminale = compréhensible par un élève de
terminale
![]()
|
INVERSION – Dispositif de Peaucellier-Lipkin L'inversion
d'une figure par rapport à un cercle
est une transformation, qui ressemble à la symétrie par rapport à
une droite. Un peu comme un miroir, mais en forme de cercle. Le dispositif de Peaucellier
illustre la propriété fondamentale de l'inversion: un cercle passant par le
centre d'inversion est transformé en droite. Le dispositif convertit un
mouvement circulaire en mouvement rectiligne. Améliorant le parallélogramme de Watt, il
est adopté sur les locomotives. |
Charles Peaucellier (1832-1919)
|
Polytechnicien, ingénieur et officier français,
connu pour avoir inventé (1864) le premier mécanisme plan transformant un
mouvement circulaire en mouvement rectiligne. Son dispositif est redécouvert en 1871
par le lituanien Lipman Lipkin. |
|
Dispositif |
|
||
|
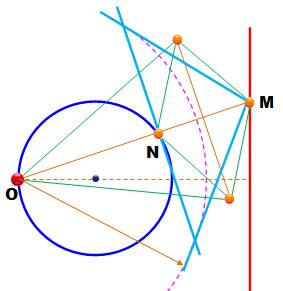
Le dispositif est constitué des barres vertes:
Le point
O est fixe; le point N décrit le cercle bleu (un arc). Alors, le point M se déplace
sur la droite M. Ces points sont liés par une inversion
de centre O et de puissance R² = a² – b² (cercle directeur en pointillés roses). |
|
||
|
Il s'agit bien d'une inversion |
ON . OM =
R² ? |
||
|
Sur la droite OM |
ON . OM = (OR – RN) (OR + RM) |
||
|
Dans le losange
RN = RM |
ON . OM = (OR – RN) (OR + RN) = OR² – RN² |
||
|
OR² = a² –
PR² et PR² = b² – RN² |
|||
|
En remplaçant |
ON . OM =
a² – PR² – (b² – PR²) = a² – b²
|
||
|
Vérification de l'inversion par
construction Les trois
lignes bleues montrent la construction classique de l'inversion du point N
par rapport au cercle directeur en pointillés roses.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()