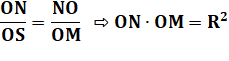|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Niveau terminale = compréhensible par un élève de
terminale
![]()
|
INVERSION avec le CERCLE L'inversion
d'une figure par rapport à un cercle
est une transformation,
qui ressemble à L'inversion est un outil mathématique bien
utile. Il est parfois plus facile de raisonner sur l'inverse d'une figure que
sur la figure elle-même. Outil très utile pour réaliser des constructions,
comme le cercle passant par deux points et
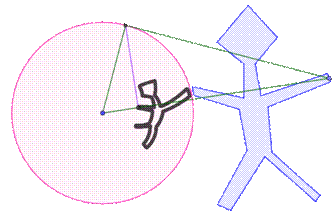
tangent à un autre cercle. Illustration: un bonhomme inversé par le cercle en rose ou
comment faire entrer le bonhomme dans le cercle ou le lion dans sa cage
(blague de mathématiciens) |
|
Le premier à avoir utilisé l'inversion fut sans doute Apollonius
de Perge (v-240 à v-180). Une
étude systématique date de vers 1924 par Jakob Steiner (1796-1863). Suivirent
d'autres mathématiciens qui s'y intéressèrent, comme William Thomson (Lord
Kelvin: 1824-1907). En 1855, August Möbius (1790-1868) édite le premier traité
exhaustif sur l'inversion. Au début des années 1910, Mario Pieri (1860-1913) écrit: Nouveaux
principes de la géométrie des inversions: une axiomatisation complète de la
géométrie d'Euclide à partir des concepts de point et d'équidistance. |
|
|
|||
|
Effets majeurs de l'inversion |
L'inversion
bascule un objet d'un côté à l'autre d'un cercle de référence. Un cercle
inversé peut devenir une droite et réciproquement. Appliquée
deux fois, l'inversion remet l'objet à sa place initiale (involution). |
||
|
P' est l'inverse de P Sur cette
figure, le point P' est l'inverse du point P par le cercle de centre 0,
cercle dit: cercle directeur (CD) ou cercle
d'inversion. Les
triangles OP'T et OTP sont semblables:
P' est l'image
de P par l'inversion
de centre (ou pôle) O et de puissance R². Construction dans un sens ou
l'autre Du point
P vers le point P' Tangente au cercle passant par P => T Perpendiculaire en T à OP => P' Ou en
inversion de P' en P: Perpendiculaire en P' à OP' => T Tangente en T => P Voir Constructions
élémentaires Tangente et autres |
Construction de l'inverse de P
Le nom OP entre deux
barres = longueur du segment OP. Propriétés Appliquer
deux fois de suite, l'inversion replace le point P à sa place de départ. Comme la
symétrie fait passer son image derrière le miroir, l'inversion fait passer
son image de l'autre côté du cercle d'inversion. |
||
|
Et si … Si P est sur le cercle son inverse est P. Le
cercle est invariant par l'inversion. Si P se rapproche de O, P' s'éloigne vers
l'infini. À la limite la tangente
en T est parallèle à OP. Sans se poser de question métaphysique ici, on
dira que l'inverse d'un point à l'infini
est le centre du cercle d'inversion. |
Le point à l'infini Par commodité, on définit un point virtuel à
l'infini qui est l'inverse du centre du cercle. Toutes les droites du plan convergent vers ce
point imaginaire à l'infini. Imaginez que nous
sommes sur la face bombée d'une goutte d'eau dont la pointe arrière s'aiguise
jusqu'à l'infini. Avec cette extension, nous
ne sommes plus totalement en géométrie
euclidienne. |
||
Propriétés
|
Prenons
deux points A et B et leurs images A' et B' par inversion, alors: angle OAB = angle OB'A' angle OBA = angle OA'B' Les
quatre points sont cocycliques car même puissance
(Feuerbach). |
|
|
|
|||
|
L'inversion de la droite par un cercle est un cercle qui passe par le
centre du cercle directeur. La figure
montre l'arc de cercle engendré par le déplacement du point sur le segment
vertical bleu. En prolongeant
le déplacement, on ferme le cercle ou presque. À la limite, le cercle se referme sur le centre du cercle
directeur. Image d'une droite sécante
Les deux points d'intersection sont leur propre image. |
Image d'un segment externe
L'arc de cercle noir est l'inversion du segment par le cercle
directeur rose. Propriété La droite passant par le centre et perpendiculaire à la droite à
inverser passe par le centre du centre image. |
||
|
Une droite passant par le centre d'inversion est invariante. Plus la droite se rapproche du centre d'inversion et plus le cercle
image est grand, jusqu'à se confondre avec la droite elle-même. |
Image d'une droite passant à
proximité du centre d'inversion
|
||
|
|
||
|
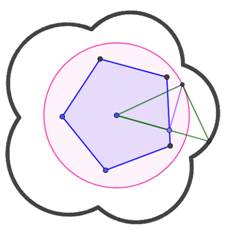
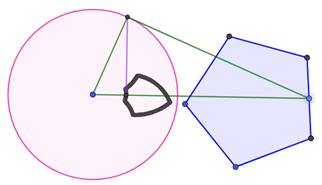
L'image
du triangle équilatéral par inversion avec un cercle et un triangle courbe. L'image
du polygone est un polygone aux côtés courbés. Image d'un polygone interne
|
Image d'un triangle équilatéral
externe
Image d'un polygone externe
|
|
Dessins réalisés avec GeoGebra
(gratuit) – Activer la fonction "trace" (clic droit sur le point)
Voir Une animation
GeoGebra sur l'inversion du cercle – Cut-The-Knot
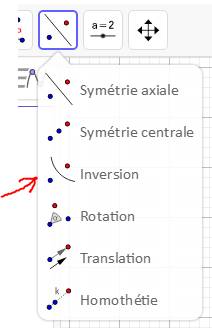
NB: GeoGebra dispose d'une instruction
inversion dans la boite à outils des transformations.
|
|
|||
|
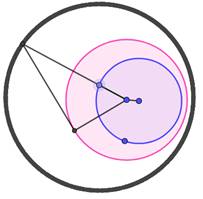
L'inversion d'un cercle est un cercle, sauf s'il passe par le centre
d'inversion. Attention: l'inverse du
centre n'est pas le centre du cercle image (pointillés). Lorsque le point sur le cercle à transformer est
interne au cercle directeur, son image est externe au cercle d'inversion. La
construction est adaptée en conséquence. Lorsque le cercle à inverser est interne au
cercle directeur, le cercle image est externe au cercle d'inversion. Les points d'intersection sont invariants. Image d'un cercle interne
|
Image d'un cercle externe
Image d'un cercle sécant
|
||
|
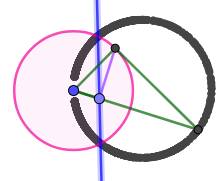
L'inversion d'un cercle qui passe par le centre d'inversion est une
droite. Si le cercle est sécant et passe par le centre, la droite-image
passe par les points d'intersection. En cas de tangence, la droite est
tangente au CD
|
Image d'un cercle passant par le
centre d'inversion
|
||
|
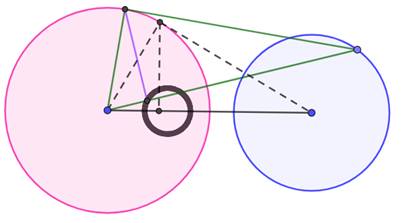
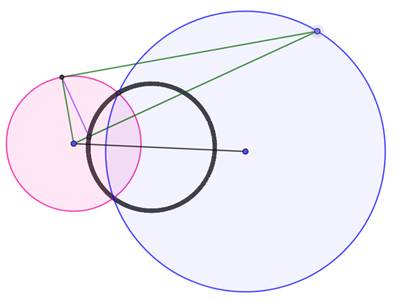
Cas de l'image de deux cercles L'inversion conserve la quantité des intersections (0, 1 ou 2). Si les deux cercles sont tangents en O, le centre d'inversion, les images
sont deux droites parallèles. Si une droite est tangente en O au cercle, l'image de la droite est
elle-même et l'image du cercle est une droite parallèle. |
|||
|
|
||
|
Cercle directeur (ou cercle
d'inversion) Un cercle directeur est invariant: il est sa propre image. L'illustration
montre l'image (noire) d'un cercle (bleu) qui se rapproche du cercle
directeur (rouge). |
Image d'un cercle proche du cercle
directeur
|
|
|
Cercles orthogonaux Un cercle orthogonal au cercle d'inversion est invariant: il est sa
propre image. Les
cercles sont orthogonaux si les rayons issus du point d'intersection sont
perpendiculaires (pointillés). Bonus Si deux cercles se coupent avec un angle alpha, leurs images se
coupent également selon un angle alpha. |
Image d'un cercle orthogonal
|
|
Bilan pour l'inversion du cercle
|
Cercle-objet |
Cercle-image |
|
Extérieur |
Intérieur |
|
Intérieur |
Extérieur |
|
Sécant |
Sécant aux mêmes points |
|
Tangent |
Tangent au même point |
|
Confondu avec le CD |
Confondu |
|
Orthogonal au CD |
Sa propre image |
|
Passe par le centre |
Droite |
|
Et, il coupe le CD |
Mêmes intersections |
|
Ou, tangent au CD |
Tangente au CD |
CD: cercle directeur
|
|
||
|
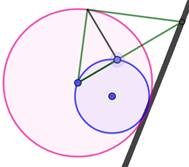
Tangentes invariantes |
1)
Tangente au CD => cercle image tangent au CD. 2)
Droite tangente à un cercle => deux cercles images sont tangents. 3)
Cercle tangent au CD => cercle image tangent au CD. |
|
|
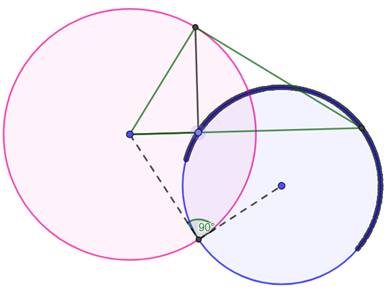
Illustration des cas de tangences
L'arc de cercle est l'image du segment vert; le cercle complet noir
est l'image du cercle bleu. Le cercle directeur est en rose. |
||
|
|
||
|
Propriété Sur cette
figure M et N sont en inversion de centre O et de puissance R². Démonstration Les triangles rectangles NOM et NPS ont
un angle commun en N. Ils sont semblables.
|
Une manière de visualiser
l'inversion
|
|
Voir Globe terrestre
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()