NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/08/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
				Quatre cercles – Construction
		Sommaire de cette page >>> Approche >>> Construction >>> Propriétés >>> Problème avec quatre cercles >>> Quatre cercles en contact

Quatre cercles

inscrits dans un triangle équilatéral

Problème de construction géométrique type Sangaku.

Comment construire la figure et calculer les proportions ?

Devinette

Avec cette configuration, quelle est la valeur de R (le rayon du grand cercle) en fonction de r (rayon des trois petits cercles) ?

Solution

Approche
Un dessin de Sangaku Le triangle équilatéral est découpé en quatre triangles tels que les cercles qui y sont inscrit sont identiques. Si le coté triangle vaut c, alors le rayon de chaque cercle est égal à: Voir ce nombre

Construction
Construction des triangles internes Un triangle équilatéral ABC. Le milieu M d'un des côtés. Perpendiculaire en M à AB Cercle (A, AB) Intersection D La droite AD supporte l'un des côtés des triangles internes. Le même procédé permet de tracer les deux autres droites
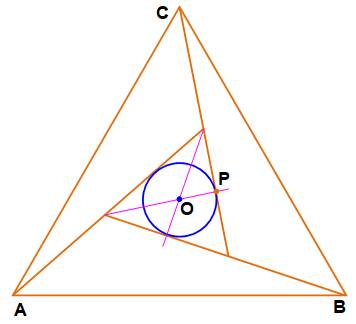
Construction des cercles Pour trouver le centre de chaque cercle, construire les bissectrices des angles. Noter le centre 0 et un point d'intersection P Tracer le cercle (O, OP). Opération à répéter pour les quatre triangles.
Construction avec GeoGebra

Voir Outils informatiques / Construction règle et compas

Propriétés
Les centres des trois cercles forment un triangle équilatéral (marron) dont le centre du quatrième est le centre (points de concours des droites remarquables). La longueur du côté vaut 4r (quatre fois le rayon des cercles). Le triangle (vert) formé par les droites internes est un triangle équilatéral de même centre. Le point de tangence d'un des trois cercles se trouve également sur le triangle marron. Le calcul du rayon n'est pas immédiat. Plusieurs solutions sont proposées par Alexander Bolgolmy.

Problème avec quatre cercles
But Avec cette configuration, quelle est la valeur de R (le rayon du grand cercle) en fonction de r (rayon des trois petits cercles) ? Solution Avec a le rayon du cercle circonscrit au triangle équilatéral (pointillés verts à droite). Rayon du grand cercle: R = r + a R = 2,154700… r	Exemple

Retour / Autres énigmes

Quatre cercles en contact
Théorème Soit quatre cercles tangents deux à deux. Les quatre points de tangence sont cocycliques.

Suite	Arbelos Carré et deux cercles tangents Cercle inscrit Chaine de Pappus Puissance d'un point par rapport à un cercle Rayon du cercle circonscrit Sangakus
Voir	Bissectrices Cercle – Index Cercles et triangles Cône Diamètre Géométrie – Vocabulaire Périmètre Sphère
Site	Four Incircles in an Equilateral Triangle, a Sangaku – Cut-The-Knot Revisiting Geometric Construction using Geogebra – ResearchGate Four Touching Circles – Cut-The-Knot
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/QuatCerc.htm