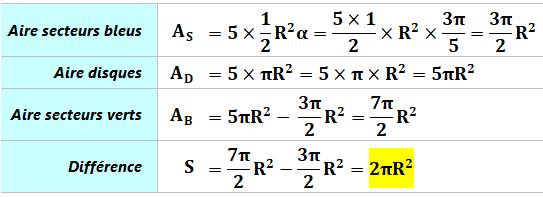|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLE et son PÉRIMÈTRE Paradoxe de la corde autour de la Terre
Vous n'allez pas le croire! Une sorte de paradoxe. On commence simplement avec
une corde en ligne droite, puis on passe au carré
pour arriver au cercle. Cette page lue, vous pourrez aller vers encore plus
incroyable: le paradoxe de la
corde soulevée. |
Voir
Paradoxe des chapelets de cercles
Anglais: The string
puzzle / Rope around the Earth problem
|
|
||
|
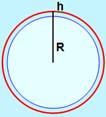
Question Sur ce
terrain de 100 mètres de long, je dispose d'une corde qui dépasse cette
longueur de 1 mètre. Un piquet
est disposé au milieu du terrain. Quel est
sa hauteur pour que la corde soit tendue ? |
|
|
|
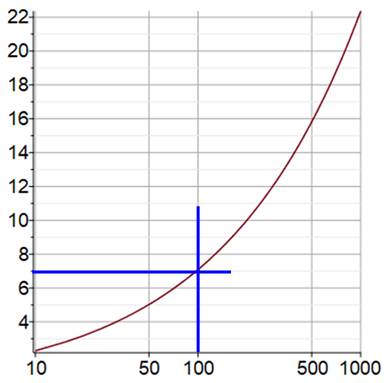
Réponse Simple,
avec le théorème
de Pythagore.
En bleu sur le
graphe. Avec un
terrain de 1 km de long et une corde dépassant toujours de 1 mètre, elle
pourrait être soulevée de 22 mètres. |
h = f (B) avec L = B + 1
|
|
Voir Brève
575
|
|
||
|
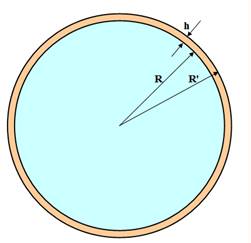
Problème Un champ de forme carrée (ou rectangulaire) est
entouré par une clôture électrique de
longueur L. On décide d'éloigner cette clôture à une distance
h des bords. La clôture est en arc de cercle aux angles. On cherche à savoir quelle est la longueur de
câble à ajouter. Réponse L'ancienne clôture en bleu se retrouve
intégralement pour former la nouvelle. Seules les parties arrondies en rouge
ont été ajoutées. En les réunissant, elle forme un cercle de rayon h. Conséquence: la clôture doit être allongée de |
|
|
|
Commentaire Il est curieux de constater que:
|
||
|
|
||||
|
Problème Une corde est posée sur l'équateur terrestre. Quelle est la
hauteur de la corde, une fois retendue ? Terre parfaitement
sphérique et corde non-élastique. Réponse Avec une corde plus longue de seulement 6 mètres, la corde peut
s'élever de 1 mètre
partout autour de la Terre. Si, si! C'est vrai ! |
|
|||
|
Calcul
Propriété En élevant la corde d'une hauteur h sur sphère, la longueur augmente
comme la circonférence d'un cercle de rayon h, quel que soit le rayon de la
sphère. Voir Corde soulevée au-dessus du cercle
/ Jeu et énigmes
|
||||
|
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
||
|
Un
cheval galope durant 10 heures. Ses pattes de gauche parcourent 10 km et
celles de droites 11 km. Expliquer! |
T = 10 h Pg = 10 km Pd = 11 km |
|
|
Non,
le cheval n'est pas un dahu. |
|
|
|
Supposons:
écart entre les pattes de droite et celles de gauche: |
h = 0,5 m |
|
|
L'écart
de parcours correspond à k tours de manège: |
|
|
|
Quantité
de tours: |
k = 1000 /
(2 x 3,14 x 0,5) = 318,3 tours |
|
|
Supposons
que le cheval galope à: |
10 km / h |
|
|
Il
a parcouru: |
10 x 10 =
100 km |
|
|
Longueur
de chaque tour du manège: |
100 /
318,3 = 0,314 km |
|
|
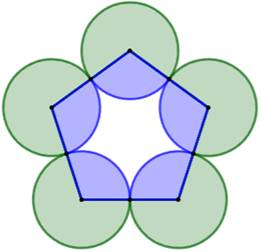
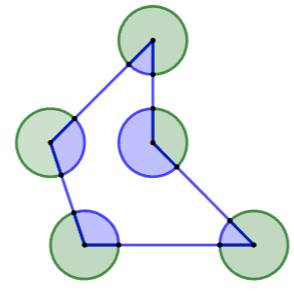
Construction Un
pentagone régulier de côté 2 cm. Cinq
cercles centrés sur les sommets et de rayon 1 cm. Aire
de a partie colorée en bleu, de celle en vert et différence. Piste L'aire
d'un secteur de disque est proportionnelle à son angle. Donc
à la somme des angles pour les cinq secteurs. Or celle-ci vaut (5 – 2) × 2π
radians. |
|
||
|
Calculs
|
|||
|
Généralisation Ce
calcul peut être répété même si:
Propriété générale et paradoxale ! Aire verte – Aire bleue = 2πR² |
|
||
|
Collier de perles La
propriété est vérifiée avec ce collier de perles: La
différence de surface entre la zone verte et la zone bleue est toujours
équivalente à l'aire de deux petites perles
quelle que soit la quantité de perles. |
|
||
Voir Brève 57-1138
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Perimetr.htm
|
![]()