|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Résolution des TRIANGLES Triangle (48°, 42°, 90°) Comment résoudre un tel triangle de façon que les longueurs des cotés
soient des nombres
entiers. Impossible! Mais comment
s'en approcher au mieux. |
|
|
||
|
Le
problème consiste à trouver un triangle en nombres entiers dont l'un des
angles mesure 48°. Le triangle de Pythagore (3,
4, 5) est un modèle: triangle rectangle dont trois côté sont en
nombres entiers. Notre
recherche consiste à trouver un triangle rectangle avec A = 48° et ses trois
côtés en nombres entiers. Autant
dire tout de suite, que ce triangle n'existe pas. |
On connait le triangle
isiaque:
Carte d'identité
|
|
|
|
|
|
L'angle de 48° correspond à un angle de 4 Pi / 15
en radian soit 0,8377… radian La valeur des lignes trigonométriques
sont irrationnelles
faisant intervenir les racines de 2, 3 et 5.
Avec de telles valeurs pas étonnant qu'il
soit difficile de trouver des nombres entiers dans le triangle. |
|
|
|
|
|
Quatre
cas examinés: 1. Angles entiers et côtés proches d'entiers; 2. Côtés entiers et angles proches des entiers imposés (48 et 90); 3. Idem; 4. Triangle rectangle avec longueurs de
côtés inférieures à 100; et 5. Côtés en entiers inférieurs à 100 et angles proches des valeurs
imposées. Carte d'identité
selon diverses contraintes (en jaune, nombre entiers)
Bilan: Les solutions 1) et 5) sont
sans doute les plus adaptées à la réalisation d'un dessin concret avec une
précision suffisante selon que l'on veut les trois côtés entiers ou les trois
angles entiers. Illustration avec le premier cas (avec
1/100 des longueurs des côtés)
Résolution (sur tableur ou avec un
logiciel de calcul) On impose un
angle (C = 90°), un côté (b = 63) et un angle (A = 48°) Soit un cas de résolution
type LAL. Essais avec
diverses valeurs des paramètres en se rapprochant d'un plus petit commun multiple des valeurs
des longueurs. |
|
|
|
|
|
On impose
le troisième côté proche d'un entier. Hors
l'angle à 48°, les autres sont quelconques. Carte d'identité avec a presque entier (la
colonne de droite montre l'écart à un entier)
Le premier est
le plus proche de l'objectif: 3762, 1000, 4357. Résolution (sur tableur ou avec un
logiciel de calcul) On impose un
côté (b = 1000), un côté (c =4357) et
un angle (A = 48°) Soit un cas de résolution
type LLA. On fait varier
les valeurs de b et c selon les lignes du tableur ou alors dans deux boucles
de programme. |
|
|
|
|
|
On impose
des nombres entiers pour les côtés. On
cherche à se rapprocher de l'angle à 48°; les deux autres angles sont
quelconques. Carte d'identité selon diverses contraintes (en
jaune, nombre entiers)
Le
premier est le meilleur selon nos contraintes. Le
dernier donne un des angles voisin de 90°. Illustration avec le dernier cas
|
|
|
|
|
|
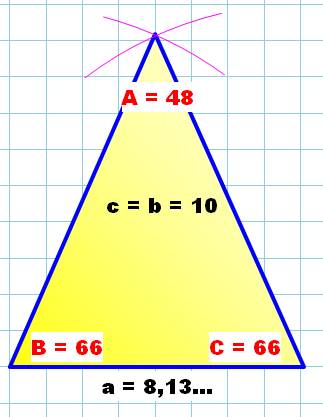
Le triangle isocèle avec 48° au sommet. Les cinq
valeurs, hors la base, sont des nombre entiers (normal!) Mais
quelle est la longueur de la base? Carte d'identité et illustration
|
|
Merci à Alain M. pour l'idée de cette
page
![]()
|
Triangles 49° et 90° |
|
|
|
Figure Triangle avec
49° et 90°, et côtés entiers (presque) en mm. Encore
plus proche des entiers avec: 926, 805 et 1 227. Tableau Il montre
les paramètres du triangle de la figure en ligne 1. Les deux
autres possibilités sont encore plus proches des entiers, mais avec des
nombres plus grands Notez que
2 = 1 zoomé d'un facteur 1,206 et que 3 = 1 zoomé par 3,07. (rapport d'homothétie). Les trois
triangles proposés sont semblables,
bien entendu. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Trg48.htm
|
![]()