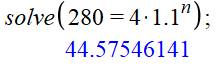|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS avec exposants Un exemple de
résolution
|
|
|
||
|
Résolution Comment résoudre une équation ayant des inconnues
au niveau des exposants. 7^(x+8) =
8^(x+7) Pour faire "redescendre" l'exposant, il
faut passer aux logarithmes. Sachant que: ax = x ln a |
|
|
|
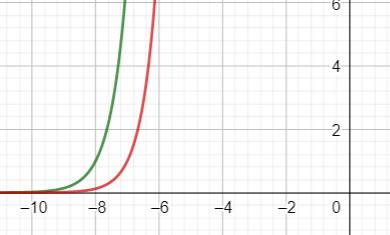
Graphes En vert: 7x + 8 En rouge 8x + 7 À cette échelle, impossible d'apprécier le point
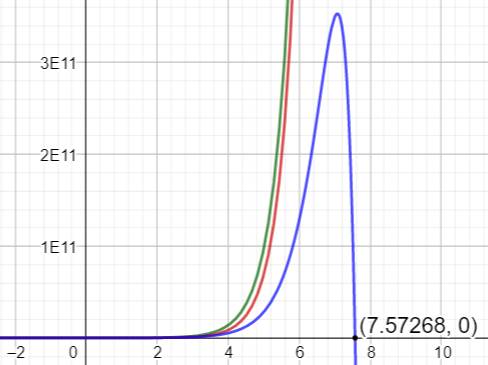
de concours et même de dire s'il existe. En bleu: la différence entre les deux courbes. Inversion de tendance de l'écart autour de 7,1
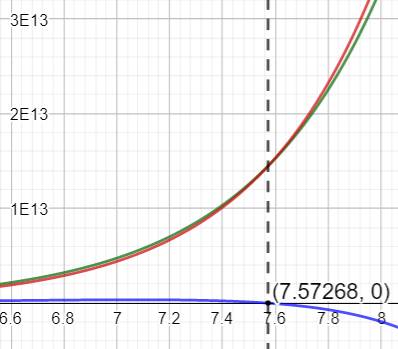
(pointe de la courbe bleue), puis passage à zéro en 7,57… En bas, le même graphe centré sur le passage à zéro de l'écart. Il illustre le fait que les deux courbes (verte
et rouge) se croisent. |
|
|
|
|
||||||||||||||||||||||||
|
Problème Il y a 4 milliards
d'internautes en 2018. Il
ya jusqu’à 280 milliards d'adresses Internet. Avec une
croissance de 10% d'internautes par an, dans combien d'années atteindrons
nous cette limite ? Résolution avec tableur Le
tableau montre que les 280 milliards sont atteints pour un peu plus de 44
années. |
|
|||||||||||||||||||||||
|
Résolution littérale Avec une augmentation
annuelle de 10%. |
…
|
|||||||||||||||||||||||
|
Pour atteindre 280 |
|
|||||||||||||||||||||||
|
Passage aux logarithmes Seule
possibilité pour "faire descendre" l'exposant) Un produit devient somme. Un exposant devient coefficient multiplicateur. |
|
|||||||||||||||||||||||
|
Calcul Utilisation
d'une calculette. |
|
|||||||||||||||||||||||
|
Ou taper
simplement (ln(280)-ln(4))/ln(1.1) dans la
fenêtre du moteur de recherche. |
|
|||||||||||||||||||||||
|
Logiciel de calcul Introduire
l'équation originelle et demander la résolution (ici: solve = résoudre en anglais). |
|
|||||||||||||||||||||||
Voir Programmation – Index
Merci à Julien pour l'idée de cette page
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()