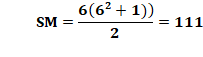Carrés magiques d'ordre 6 à partir du 3x3

Comment profiter de la construction d'un carré magique 3x3 (ordre impair, réputé simple à construire) pour façonner un carré 6x6 (ordre pair, généralement plus compliqué à construire).

Voir de suite les quatre solutions à deux permutations >>>

Cette méthode peut aussi s'interpréter comme une addition de matrices >>>

Anglais: Construct a 6x6 Magic Square with a 3x3 Magic Square

Un carré magique 3x3

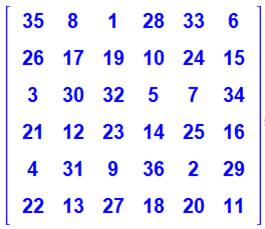
Le carré 3x3 est construit dans un canevas de 6x6.

On retrouve la méthode classique de construction:

montée en diagonale et enroulement au delà des bordures

descente d'un cran aux multiples de 3.

Un carré initial 6x6 – Presque magique
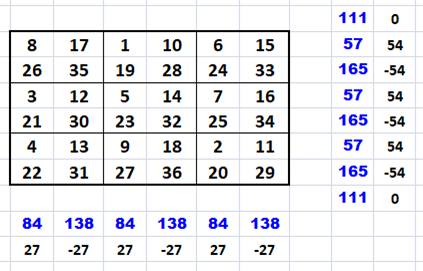
Le carré 3x3 initial est répété quatre fois avec les nombres de 1 à 36, "enroulés" sur l'ensemble du carré La somme magique vaut: Cette construction simple s'approche de la solution. On constate: écart alterné de 54 sur les lignes; écart alterné de 27 sur les colonnes; et sommes correctes sur les diagonales.	Chaque zone 2x2 est complétée par trois nombres augmentés de 9. En bleu la somme des lignes, colonnes et diagonales. À côté, les écarts par rapport à la somme magique.
Idée ? Permuter les nombres dans les zones 2x2.	On se dit que la solution est à portée de main. Pas si sûr ! Une simple permutation générale dans les zones 2x2 ne parvient pas à combler les écarts. Il faut procéder à des permutations sélectives.

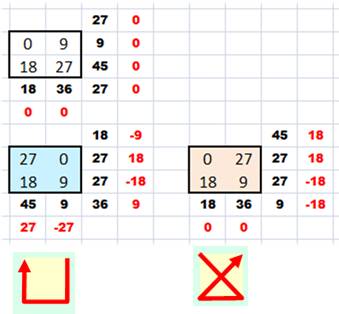
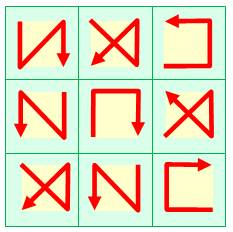
Deux solutions 6x6 avec seulement deux permutations
L'astuce de construction Voici deux permutations d'une zone 2x2 avec l'originale en blanc. On a indiqué les écarts. En prenant les nombres en ordre croissant: en bleu, une disposition en U inversé; et en marron, une disposition en croix. Les nombres latéraux en rouge indiquent quelle est la variation par rapport à la zone originale, en ligne comme en colonne. Par exemple, en optant pour une disposition en U (bleu), on modifie les lignes de 18, les colonnes de 27 et les diagonales de 9. 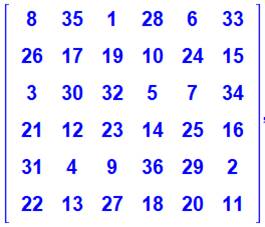*Reste à réfléchir à un jeu de "pesée" pour combler les écarts.* *Il s'agit de sélectionner les écarts pour atteindre les différences en ligne et en colonne du carré magique complet.*		Les deux permutations utilisées
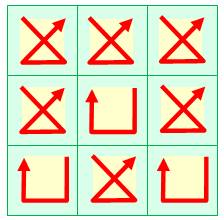
Deux seules solutions En fait, deux solutions symétriques par rapport à un axe horizontal. Présence de trois U qui atteignent l'écart 27, nécessaire en colonne. Les trois permutations, l'une ou l'autre, engendrent 3 x 18 = 54 qui comble l'écart sur les lignes Reste à neutraliser les diagonales avec deux U (2 x 9) et un X (18).
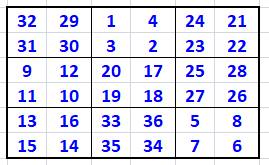
Variantes Au lieu d'enrouler les nombres quatre fois sur le carré complet, on peut aussi les enrouler dans le carré 2x2. Avec les mêmes permutations, on obtient deux nouveaux carrés magiques.
Autres solutions	En profitant des 24 permutations des quatre nombres des carrés 2x2, il est possible de trouver des milliers de carrés magiques 6x6. J'ai stoppé l'exploration à 4 000 réponses alors que le programme en était toujours à la même première ligne. Avec les permutations du carré 3x3 d'origine, on multiplie encore la quantité de solutions.

Voir Méthode appliquée à la création du carré 10x10

Méthodes matricielles
Principe de construction La méthode par doublement peut s'interpréter comme une addition de carrés (matrices): Le premier tableau est le carré 3x3 quadruplé; Le deuxième reflète les permutations utilisées comme indiqué par nos traits fléchés et traduit en nombre (0, 1, 2 et 3); et Le troisième est la somme du premier et neuf fois le deuxième.	Un exemple de permutations qui marchent
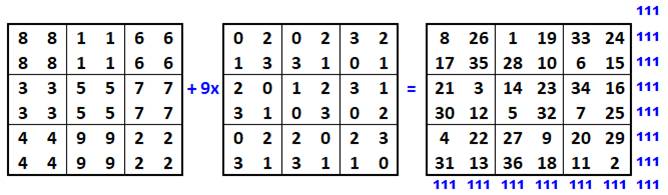
"CM 3x3" + 9 (tableau de permutations) = "CM 6x6" Exemples de calcul: 8 + 9 x 0 = 8; 8 + 9 x 2 = 26; 1 + 9 x 0 = 1; 1 + 9 x 2 = 19; etc.

Méthode matricielle par copies du carré moitié

Le premier tableau est constitué du carré magique 3x3 copié quatre fois;

Le deuxième est composé des coefficients multiplicateur 0, 1, 2 et 3, disposés judicieusement; et

Le troisième est la somme du premier et neuf fois le deuxième.

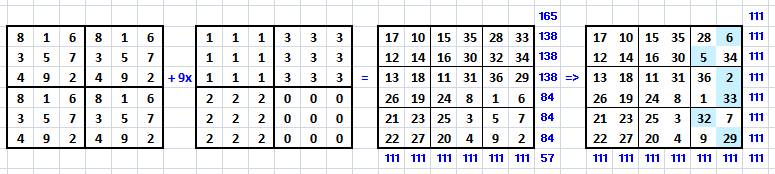
Le tableau intermédiaire est constitué d'un carré en 1, d'un carré en 2 et de deux carrés panachés en 0 et 3.

Avec ces derniers, on veille à satisfaire la somme en diagonale, puis les sommes en lignes et en colonnes.

Méthode matricielle équivalente

Le premier tableau est constitué du carré magique 3x3 copié quatre fois;

Le deuxième est composé des coefficients multiplicateur 0, 1, 2 et 3 par quadrant; et

Le troisième est la somme du premier et neuf fois le deuxième.

Le quatrième et identique à trois permutations près

Le tableau final est identique au précédent, sauf les nombres en bleu qui sont intervertis.

Comment les choisir ?

On commence par rétablir les diagonales en intervertissant deux fois des nombres ayant une différence de 27.

Avec les seules possibilités pour les diagonales, il se trouve que les sommes en ligne sont aussi satisfaites.

Ce carré magique est identique au précédent.

Permutations utilisées: carrés magiques et diagrammes des permutations

La ligne fléchée indique le sens croissant des nombres dans un carré 2x2

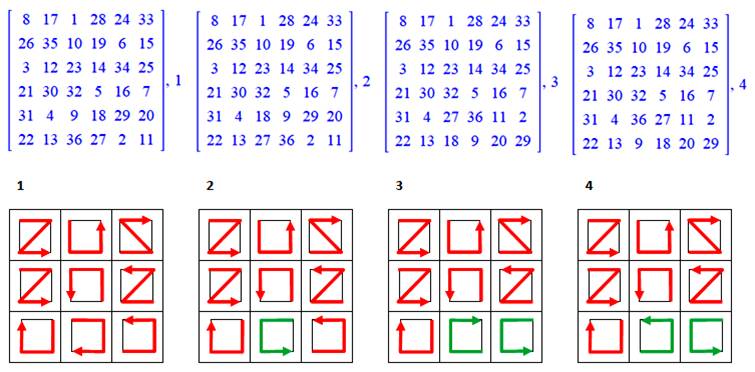
Florilège (à gauche, le rang selon les permutations utilisées

Programmation Maple
	Commentaires Appel de logiciels de calcul matriciel (Array) et de calcul combinatoire. Liste (eij) des nombres dans chaque carré 2x2 et calcul des permutations (Eij). Boucles d'analyse des permutations successives et formation de la matrice 2x2 des nombres permutés (aij). Pour accélérer la recherche, on teste les deux premières lignes formées par f, g et h. On forme la matrice A en concaténant les trois premières matrices 2x2. On obtient une matrice 2x6. SL est la liste des sommes des lignes. Si les deux valent la somme magique 111, on poursuit l'exploration. Même procédé pour les deux lignes suivantes. On teste les lignes 3 et 4 et on poursuit si elles valent 111. Après formation des deux dernières lignes avec les trois boucles en l, m et n, on forme la matrice complète A. On forme l'ensemble (set) des sommes en ligne et en colonne. Si les nombres sont identiques, l'ensemble ne comporte que ce nombre unique (nops () = 1). On calcule la somme sur chaque diagonale (SD1 et SD2). Si ces sommes sont 111, on édite la matrice et son numéro (kt).
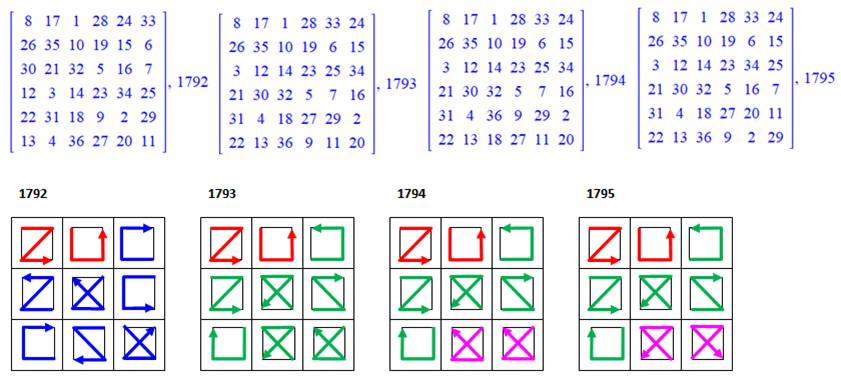
		Les deux prières réponses du programme:

Voir Programmation – Index

Suite	Méthode appliquée à la création du carré 10x10 Carré 6x6 en devinette Carré d'ordre 7 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Énigmes Jeux Nombres en chiffres Nombres magiques - Index Rubriques débutants Sudoku
Diconombre	Nombre 6 Nombre 36 Nombre 111 Nombre 666
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre6.htm