|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres et leurs chiffres en puissance Trouvez des
égalités entre deux nombres et la somme des puissances de leurs chiffres. 136 = 23 + 43
+ 43 & 244 = 13 + 33 + 63 919 =
13 + 43 + 53 + 93 & 1459 = 93 + 13
+ 93 ou encore 193 = 6 859
& 6 + 8 + 5 + 9 = 28 283 = 21 952 &
2 + 1 + 9 + 5 + 2 = 19 |
|
|
||
|
soit égale
|
Narcissique 153 = 13 + 53 + 33 Exemples 23 et 139 23 + 33 = 1 + 3 + 9
= 13 21 et 322 24 + 14 = 32
+ 22 + 22 = 17 136
= 23 + 43 + 43 & 244 = 13 + 33
+ 63 |
|
|
|
||
|
|
|
|
|
|
SA
= ap + bp + cp SE
= eq + fq + gq |
|
|
Égalité de la somme des chiffres en puissance. |
SA = SE |
|
|
Somme des chiffres en puissance de l'un égale à l'autre nombre. |
A = SE &
E = SA |
|
|
|
|
|
|
|
SAa
= rp + sp + tp + … SEb
= uq + vq + xq + … |
|
|
Somme des de l'un à une puissance égale à l'autre nombre. |
SAa = SEb |
|
|
Somme des de l'un à une puissance égale à l'autre nombre. |
A = SEb &
E = SAa |
|
|
Illustration |
|
|
|
|
|
|
|
|
Exemples au hasard 12
et 14 => 14 + 24
= 12 + 42 = 17 22 et 44 =>
24 + 24 = 42 + 42 = 32 192 et 378
=> 14 + 94 + 24 = 34 + 74
+ 84 = 6 578 999 et 603
=> 92 + 92 + 92 = 63 + 03
+ 33 = 243 921 et 763
=> 94 + 24 + 14 = 74 + 64
+ 34 = 6 578 Vous
noterez que ces égalités restent valables si on permute les chiffres: 94
+ 24 + 14 = 14 + 94 + 24 Exemples triviaux 998 et 989 => 9
+ 9 + 8 = 9
+ 8 + 9 =
26 998 et 989 => 92 + 92 + 82
= 92 + 82 + 92 = 226 998 et 989 => 93 + 93 + 83
= 93 + 83 + 93 = 1970 Si la somme des entiers est égal, normal que les
sommes des mêmes puissances soient égales. Il est possible de former une telle égalité avec
pratiquement tous les nombres et en plusieurs motifs. Les nombres suivants
font exception: 10, 11, 16, 20, 26, 30, 37, 40, 46, 50, 60, 61, 62, 64, 68,
70, 73, 79, 80, 86, 89, 90, 97, 98, 100, 101 … |
|
|
|
|
|
136 = 23 + 43
+ 43
& 244 = 13 + 33
+ 63 919 =
13 + 43 + 53 + 93 & 1459 = 93 +
13 + 93 2 178 = 64 + 54
+ 14 + 44
& 6 514 = 24 + 14
+ 74 + 84 58 618 = 75 + 65
+ 45 + 35 + 85 & 76 438 = 55 + 85
+ 65 + 15 + 85 Voici le bilan en tableau (vous y
reconnaissez les couples cités ci-dessus)
|
|
|
|
|
|
CUBES
2
=> 23 = 8 & 200
=> 2003 = 8 000 000 => 8
2
=> 23 = 8 & 5
=> 53 = 125 => 8 2
=> 23 = 8 & 8
=> 83 = 512 => 8 3
=> 33 = 27 => 9 &
6 => 63 = 216 => 9 9 => 93 = 729 => 18 &
81 => 813 = 531 441 => 18 12
=> 123 = 1728 => 18 &
24 => 243 = 13 824
=> 18 12
=> 123 = 1728 => 18 &
48 => 483 = 110 592 => 18
4 => 43 = 64 => 10 &
7 => 73 = 343 => 10 14
=> 143 = 2 744 => 17 &
17 => 173 = 4 913 => 17 14
=> 143 = 2 744 => 17 &
23 => 233 = 12 167 => 17 9 => 93
= 729 => 18
& 12
=> 123 = 1 728 => 18 9 => 93
= 729 => 18
& 15
=> 153 = 3 375 => 18 13
=> 133 = 2 197 => 19 &
16 => 163 = 4 096 => 19 13
=> 133 = 2 197 => 19 &
22 => 223 = 10 648 => 19 13
=> 133 = 2 197 => 19 &
25 => 253 = 15 625 => 19 19
=> 193 = 6 859 => 28 &
31 => 313 = 29 791 => 28 … |
|
|
|
||
|
Carrés Cubes Bicarrés Puissance 5 |
132 = 169 &
1 + 6 + 9 = 16 16² = 256 &
2 + 5 + 6 = 13 193 = 6 859
& 6 + 8 + 5 + 9 = 28 283 = 21 952 &
2 + 1 + 9 + 5 + 2 = 19 184 = 104 976 &
1+0+4+9+7+6 = 27 274 = 531 441 &
5+3+1+4+4+1 = 18 235 = 6 436 343 & 6+4+3+6+3+4+3 = 29 295 = 20 511 149
& 2+0+5+1+1+1+4+9 = 23 315 = 28 629 151
& 2+8+6+2+9+1+5+1 = 34 345 = 45 435 424
& 4+5+4+3+5+4+2+4 = 31 |
|
|
Puissance 6 Puissance 7 Puissance 8 Puissance 9 |
/ 38 & 47 => 114415582592, 506623120463 44 & 62 => 319277809664, 3521614606208 46 & 55 => 435817657216, 1522435234375 56 & 65
=>
1727094849536, 4902227890625 Coquetterie
avec chiffres retournés 64 & 73 => 281474976710656,
806460091894081 35 & 80 => 78815638671875,
134217728000000000 |
|
|
Puissances croisées |
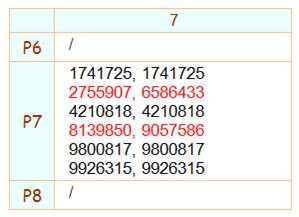
255,
408, Rappel:
cela veut dire que la somme des chiffres de 976… est égale à 40 et celle de
655… est égale à 25. 255,
4011, 466,
647, 729,
9910, 739,
9110, 629,
7111, 5210,
7013, 6311,
9013, 62050608388552823487, 6311,
9015, 62050608388552823487, 6311,
9016, 62050608388552823487, 8111,
9018, 984770902183611232881, |
|
À la recherche
de pépites avec les chiffres des
couples de nombres portés à une puissance, les trouvailles sont rares. Elles
ne sont guère plus nombreuses que celles indiquées en introduction. Par contre,
lorsqu'il s'agit de l'égalité entre un nombre et la somme des chiffres de la
puissance d'un autre, la moisson est plus fructueuse. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Puissanc.htm |
![]()