|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIPLICATIONS RAPIDES par 5, 6, 7, 8, 9, 11 & 12
Lorsque le
multiplicateur est compris entre 5 et 12, il y a C'est
une méthode qui applique un algorithme
simple pour calculer chaque chiffre du
résultat à partir de ceux du multiplicande. |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 11 = 13 574
Exemples avec écriture
abrégée
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 12 = 14 808
Exemples avec écriture
abrégée
Le chiffre indicé indique
qu'il y a une retenue. |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 5 = 6 170
Exemples avec écriture
abrégée
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
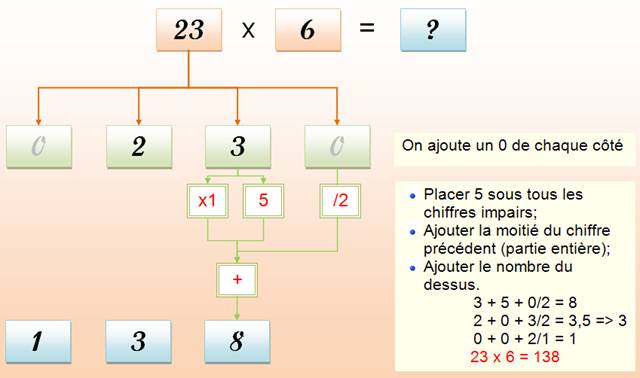
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 6 = 7 404
Exemples avec écriture
abrégée
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 7 = 8 638
Exemples avec écriture
abrégée
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 8 = 9 872
Chaque
chiffre = somme (algébrique) des chiffres de la zone en jaune Exemples avec écriture
abrégée
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Méthode de calcul illustrée
Règle en abrégé
Exemple: Calculons:
1 234 x 9 = 11 106
Exemples avec écriture
abrégée
|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette
page |
![]()