NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/07/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Nombres de Kimberling	Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Terquem / Gergonne		Démo fallacieuse
		Sommaire de cette page >>> Les six points de Terquem >>> Le point de Gergonne >>> Cercle inscrit

Voir Propriétés fondamentales des triangles

Point de Terquem ou de Reuschle

Point de Gergonne

Un double faisceau de céviennes concourantes engendre six points cocycliques: les points de Terquem.

Confondus ces deux faisceaux se rencontrent en un unique point: point de Gergonne.

Olry Terquem (1782-1862) – Mathématicien français

Karl Gustav Reuschle (1812-1875) – Mathématicien allemand

Joseph Gorgonne (1771-1589) – Mathématicien français

Cévienne: toute droite issue d'un sommet du triangle

Les six points de Terquem
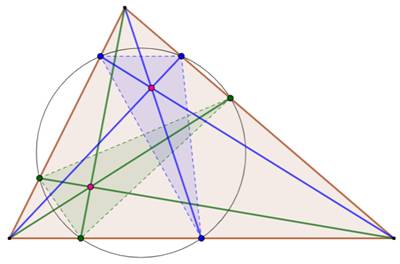
Construction Un triangle quelconque et un jeu de céviennes concourantes (vert). Le cercle passant par les trois pieds des céviennes qui recoupent le triangle en trois points. Ceux-ci sont les pieds d'un nouveau jeu de trois céviennes concourants (bleu). Les six pieds cocycliques sont les points de Terquem.

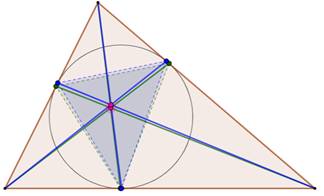
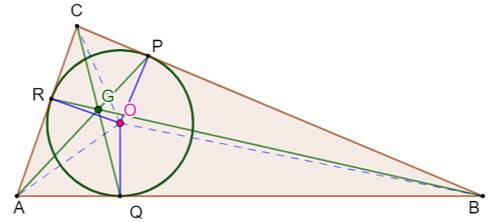
Faisceaux de céviennes confondus Avec les deux jeux de céviennes confondues, l'unique point de concours est le point de Gergonne. Le cercle est alors inscrit dans le triangle.

Cercle inscrit En trait roses, les bissectrices et leur point de concours, centre du cercle inscrit (point rouge). En vert, les deux faisceaux de céviennes superposées Les trois points doubles de Terquem sont aussi le pied des perpendiculaires aux côtés issues du point de Gergonne (point vert).
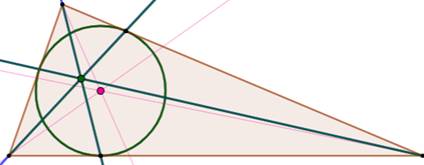
Point de Gergonne Plus simplement, le point de Gergonne est le point de concours des céviennes issues des points de tangence du cercle inscrit. Les bissectrices servent à construire le centre du cercle inscrit. Leurs points de rencontre ne sont pas les points de tangence.	Voir Bissectrices et point de Gergonne
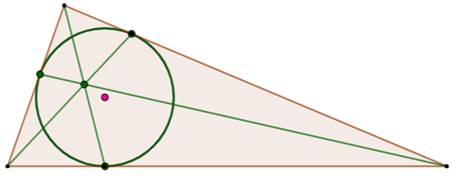
Triangles rectangles En dessinant les perpendiculaires issues du point 0, on fait apparaitre les triangles rectangles congruents (égaux) deux à deux (ex: AOR et AOQ). (Propriété générale du cercle inscrit).

Nadel et Gergonne

Le point de Nagel et le point Gergonne sont les points de concours de deux faisceaux de trois céviennes remarquables.

Ces droites relient les sommets du triangle d'origine aux points de tangence:

du cercle inscrit (Gergonne), et

des cercles exinscrits (Nadel).

Ces deux points sont des conjugués isotomiques (symétrie de construction via les milieux des côtés).

They both involve cevians drawn from a vertex to the points of tangency of circles.

Suite	Point de Brocard Points remarquables du triangle Droite d'Euler Droite de Simson Nombres de Kimberling
Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre
Sites	Théorème de Terquem – Wikipédia La géométrie du triangle – Points caractéristiques – Patrice Debart Cyclocevian Conjugate – Wolfram MathWorld Terquem's Theorem – Cut-The-Knot (Java Applet)
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Terquem.htm