|
Édition du: 28/03/2025 |
|
INDEX |
MÉTHODE de NEWTON |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Méthode de Newton avancée (2025) En mi-2024, (publication
2025 par les journaux) trois
mathématiciens inventent un algorithme
améliorant la méthode de recherche de solutions dite de Newton en l'étendant
aux équations
de degré élevé et multivariables. |
||
|
|
Sommaire de cette page >>> Approche >>> Méthode de Newton – Approximation de Taylor >>> Algorithme de Newton >>> Efficacité et lacunes >>> Méthode avancée |
Débutants Glossaire |
|
Recherche de minimum Les fonctions
mathématiques produisent des résultats (sorties) à partir de données
particulières (entrées). Souvent, on cherche à connaitre les données
d'entrée qui produiront le résultat minimum. Mais
trouver ce minimum est difficile, surtout si les fonctions sont complexes: nombreuses
variables ou encore puissances élevées. Une solution analytique, donnée par une formule,
est impossible. Une solution graphique présente des "paysages"
souvent impossibles à appréhender La méthode consiste alors à réaliser des
approximations par itérations successives. |
Image Les fonctions selon leurs entrées sont
comparables graphiquement à un relief, un paysage formé de monts et de
vallées. La question posée consiste à trouver le point le
plus bas de ce relief sans se retrouver dans le fond d'une vallée locale. La méthode de Newton consiste à estimer un point
supposé bas et à tester son environnement: "ça descend" encore, on
continue; "ça monte", on revient en arrière. |
|
|
Approximation
de Taylor |
||
|
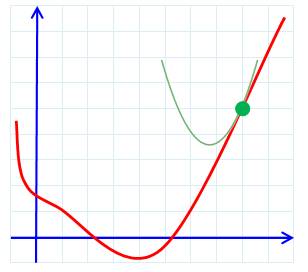
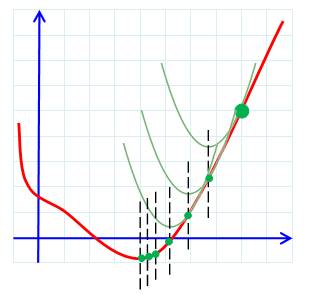
Recherche de minimum Explication du principe de la méthode de Newton dans un cas très simple: une courbe
dans le plan. La fonction est représentée par la courbe rouge. À
l'œil, le minimum est évident, mais pour un ordinateur ? La méthode consiste à choisir (estimation, intuition
!) un point sur la courbe (vert). On cherche la courbe
simple (ici une parabole en vert) qui approxime au mieux la courbe dans le voisinage
du point. On note le point bas de la parabole et on
reporte ce point sur la courbe (en abscisse, pointillé noir). C'est un
nouveau point qui s'approche de la solution (vert) On recommence la procédure avec ce nouveau point
vert et ainsi de suite jusqu'à converger vers un point stable, le point cherché. Théorème de Taylor – Approximation de
Taylor Le théorème
de Taylor (ou formule de Taylor) indique qu'une fonction plusieurs fois
dérivable au voisinage d'un point peut être approchée par une fonction polynomiale dont les coefficients
dépendent uniquement des dérivées
de la fonction en ce point. Cette fonction polynomiale est parfois appelée polynôme de Taylor. |
Illustration
|
|
|
Dérivées première et seconde Dans les années 1680, Newton a reconnu que même
lorsque vous avez affaire à une fonction très compliquée, vous aurez toujours
accès à au moins deux éléments d'information pour vous aider à trouver sa
vallée la plus profonde. Trouver les minimas sur la fonction d'origine est
compliqué; trouver les minimas sur les fonctions dérivées est beaucoup plus
facile. |
|
|
Voir Brève
62-1224
|
La méthode de
Newton est peut-être l'un des algorithmes d'optimisation les plus connus et
les plus importants. Pour minimiser une fonction f, cet algorithme remplace f
par son développement de Taylor du second ordre à un point xk
itéré et il définit xk+1 à l'itération suivante lequel devient le nouveau
point de cette approximation quadratique.
Ce point critique coïncide, en effet, avec une minimisation de
l'approximation quadratique. Le travail
requis à chaque itération de la méthode de Newton consiste à résoudre un système
d'équations linéaires qui résulte de l'annulation du gradient (c.a.d. trouver le point
minimum) de l'approximation quadratique. |
|
La méthode de
Newton est extrêmement puissante. Elle est encore cruciale pour résoudre les
problèmes actuels dans la logistique, la finance, la vision par ordinateur et
même les mathématiques pures Elle présente
également une grave lacune. Elle ne fonctionne pas bien sur toutes les
fonctions. Les mathématiciens ont donc continué à étudier la technique, en
trouvant différentes façons d'en élargir la portée sans sacrifier
l'efficacité. Note D'autres
méthodes itératives, comme la descente de
gradient (l'algorithme utilisé
dans les modèles d'apprentissage
automatique d'aujourd'hui) convergent vers le minimum réel à une vitesse
linéaire. La méthode de Newton converge beaucoup plus vite, à un rythme quadratique. |
|
Historique En
mi-2024, trois chercheurs
ont
étendu la méthode de Newton pour travailler efficacement sur la classe de
fonctions la plus large possible. Leur
algorithme fonctionne pour un nombre quelconque de variables et jusqu'à de nombreuses
dérivées, tout en restant efficace dans tous ces cas. |
Deux propriétés
Les
trois mathématiciens ont trouvé comment utiliser une technique appelée
programmation semi-définie (semidefinite programming) pour adapter
l'approximation de Taylor de manière à en faire à la fois une somme de carrés
et la rendre convexe; et cela, tout en respectant la fonction initiale à
laquelle elle est censée ressembler. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |