|
|||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 12 Critères de
divisibilité, cas de divisibilités inattendues, et formes polynomiales
divisibles par 12. Propriété
spectaculaire!
12 divise toujours le
produit des différences de quatre nombres >>> |
Voir Nombre 12 dans le
DicoNombre
|
|
|||
|
Le nombre
doit d'abord être pair. Moyen facile d'éliminer tous les impairs d'un
coup d'œil. |
144 est pair |
||
|
Il est divisible par 3. |
1 + 4 + 4 = 9 divisible par 3 |
||
|
Il est divisible par 4. |
44 est divisible par 4 |
||
|
Divisible
à la fois par 3 et par 4, ce nombre est divisible par 12 |
144 = 12 x 12 |
||
|
Autre
exemple |
1 481 472
|
||
Voir Multiplication
rapide par 12
|
|
||
|
Prenons
les quatre premiers nombres (dans les
carrés) et calculons la différence entre chaque couple (les six segments bleus et rouges). Le
produit de ces différences est égal à 12. |
|
|
|
Prenons
d'autres nombres quelconques mais distincts. Ils sont disposés dans l'ordre
croissant pour l'esthétique. Le
produit de toutes les différences est encore divisible par 12. |
|
|
Voir Divisibilité
par 12 de quatre cubes
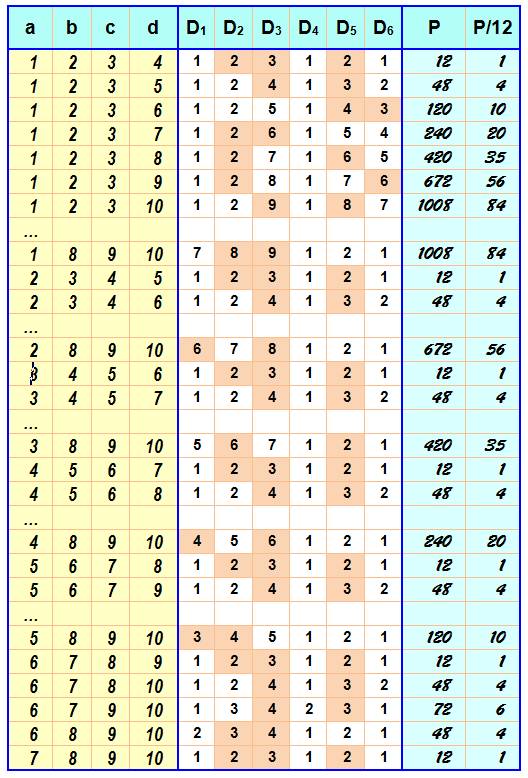
Quelques exemples: le
produit des différences est toujours divisible par 12
a, b, c et d sont les quatre nombres;
les six Di sont les différences; P est le produit des six
différences.
En marron, les facteurs qui produisent
12 ou un multiple.
|
|
||
|
Théorème Le produit de toutes les différences entre quatre nombres distincts
est divisible par 12. Distincts,
car deux nombres égaux produiraient une différence nulle qui mettrait a zéro
le produit. D'une
manière générale Le PGCD des produits des
différences de quatre nombres quelconques distincts est égal à 12. |
Formulation
La barre
verticale se lit: " divise". Soit: douze divise le produit P formé
des différences indiquées avec a, b, c et d, quatre nombres entiers dans
l'ordre croissant. Note: si
non croissant, prendre la valeur
absolue des différences. Plus
grand commun diviseur de tous les produits
Le nombre 12 est bien la limite. C'est le plus grand nombre qui divise
l'infinité de tous ces produits. Ce que montre le tableau
ci-dessus. |
|
|
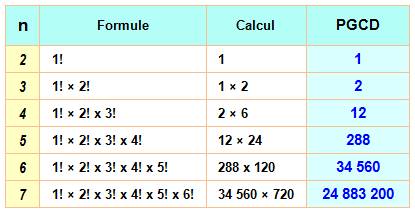
Généralisation Le PGCD des produits des différences de n nombres quelconques
distincts est égal à 1! x 2! x 3! x …
(n-1)! Distincts,
car deux nombres égaux produisent une différence nulle qui met a zéro le
produit. On peut
formuler également: Le
produit des différences deux à deux de n nombres est un multiple de
1!x2!x…(n-1)! Let a0, a1, a2,…,
an be any n + 1 integers. The product of their pairwise
differences is a multiple of 0! 1! ... n! |
PGCD des
produits pour n nombres
Voir Super factorielle Historique: en 1892, H.W. Segar
avait constaté que le produit des différences de n entiers est divisible par
2! x 3! x … (n-1)! Rapporté par Dickson. |
|
Voir Factorielle
/ Divisibilité
du produit de nombres consécutifs
|
|
||
|
Deux
temps pour la démonstration. |
Divisibilité par 2 puis divisibilité par 4. |
|
|
Outil
principal: le principe
des tiroirs. |
Avec quatre objets pour trois tiroirs, l'un des tiroirs contiendra au
moins deux objets. |
|
|
On
reprend la présentation en graphe
en l'orientant pour pouvoir y pratiquer des sommes vectorielles. Les
nombres sont dans l'ordre croissant: a < b < c < d; et, les flèches
pointent vers un plus grand nombre. Chaque
vecteur représente une différence comme (a – b) pour le vecteur horizontal
supérieur. De sorte
que, par exemple: (a – b) + (b – d) = (a – d) |
La flèche de a vers b représente la différence a – b |
|
|
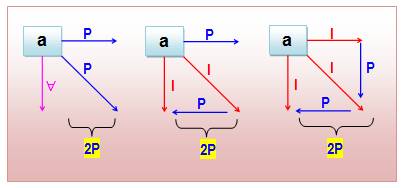
Divisibilité
par 3 On
s'intéresse au sommet "a" duquel partent trois vecteurs. Deux cas
possibles
Dans le
premier cas, le produit complet est divisible par 3; dans le second cas, il
faut montrer que cette situation engendre une autre différence divisible par
3. Rappel: la division par 3 peut donner trois types de
restes:0, 1 ou 2. On dit que qu'en mod 3,
la différence vaut 0, 1 ou 2. |
Si, issue du sommet "a", aucune différence n'est divisible
par 3, on a:
D'après le principe des tiroirs, trois cas pour deux possibilités, alors deux différences sont
soit à 1 soit à 2 mod 3. Par exemple:
Or, nous avons la somme: (a – b)
+ (b – d) = (a – d)
1 + 0 =
1 mod 3 Cette relation impose que l'une des différence soit égale à 0 mod 3; ce
qui veut dire que cette différence est divisible par 3. Il existe donc
toujours une différence divisible par 3, et le produit complet est divisible
par 3. Ce raisonnement s'applique à toutes les configurations possibles pour le
sommet "a". |
|
|
Divisibilité
par 4 Toujours
avec le sommet "a", il faut identifier deux vecteurs pairs (deux
différences paire) pour obtenir la divisibilité par 4. Trois
cas:
Conclusion Divisible à la fois par 3 et par 4, le produit est divisible par
12 ∎ |
Avec deux ou trois différences paires
émanant du sommet "a", nous avons immédiatement notre divisibilité
par 4. Avec une seule différence paire,
les deux autres sont impaires et leur différences est paire (même principe de somme et différence de vecteurs
utilisé ci-dessus). Avec trois différences impaires, on réalise deux somme/différences qui
sont paires. Illustration
|
|
Produit de différences
|
Le
produit de différences est noté
Δn is the product of the difference of all ordered
pairs of (x1, x2, …, xn) where the index of
the first is less than the index of the second. |
![]()
|
|
Voir Règles générales de divisibilité
|
Démonstration par induction |
|
|||||||||||||
|
|
p =
2k + 1 p' = 2k + 1 + 2 = 2k + 3 p + p' = 4 k + 4 = 4 (k + 1) |
|||||||||||||
|
|
4 |
|||||||||||||
|
|
|
|||||||||||||
|
|
p + p' = 3h + 2 + 3h + 4
= 6h + 6
= 6 (h + 1) |
|||||||||||||
|
|
6 |
|||||||||||||
|
|
4 = 2 x 2 6 = 2 x 3 PPCM(4,6) = 2 x 2 x 3 = 12 |
|||||||||||||
|
|
12 |
|||||||||||||
Voir Démonstration via la barre magique des
premiers
|
|
|
|
p p'
p + p' (p+p')/12 5 7 12 1 11 13 24 2 17 19 36 3 29 31 60 5 41 43 84 7 59 61 120 10 71 73 144 12 101 103 204 17 107 109 216 18 137 139 276 23 149 151 300 25 179 181 360 30 191 193 384 32 197 199 396 33 227 229 456 38 239 241 480 40 269 271 540 45 281 283 564 47 311 313 624 52 347 349 696 58 419 421 840 70 431 433 864 72 461 463 924 77 521 523 1044 87 569 571 1140 95 |
|
![]()
|
Suite |
|
|
Diconombre |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi12.htm
|
![]()