Brèves de maths 02

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/01/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 2

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

20. Dix en chiffres
Faire 10 avec des 1 Comment écrire le nombre 10 avec le moins possible de bâtons. Les quatre opérations et les parenthèses sont autorisées. Plusieurs possibilités: Maximum 10 bâtons et minimum 7 bâtons avec l'opération: 3 x 3 + 1 = 10.		Faire 10 avec chacun des chiffres Si le bâton représente le chiffre 1, comment poursuivre avec les autres chiffres de 2 à 9.
Brèves associées	>>> 2018 et ses chiffres
Pour en savoir plus	>>> Nombres >>> Chiffres		>>> Tous les jeux du même type >>> Le célèbre quatre 4

21. Somme: 1 + 2 + 3 + 4 + …
Sommes sympathiques 1 + 2 + 3 + 4 = 10 1 + 2 + 3 + … + 11 = 66 1 + 2 + 3 + … + 36 = 666 1 + 2 + 3 + … + 114 = 6555 Somme jusqu'à 10 – Attention astuce! 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 Cette somme est plus facile à calculer en faisant: 1 + 9 + 2 + 8 + 3 + 7 + 4 + 6 + 5 + 10 = 55 Encore plus malin: 1 + 10 + 2 + 9 + 3 + 8 + 4 + 7 + 5 + 6 = 5 x 11 Légende On dit que Gauss à 10 ans aurait utilisé cette astuce pour faire un tel calcul, demandé par un professeur qui souhaitait avoir un moment tranquille avec ses élèves. Sommes amusantes 1 + 2 + 3 + … + 100 = 50 50 1 + 2 + 3 + … + 1000 = 500 500 1 + 2 + 3 + … + 10 000 = 5000 5000		Disposition pratique La somme est écrite à l'endroit, puis à l'envers. On effectue la somme en colonnes. Il a 10 colonnes et chaque somme vaut 11 (=10 + 1). Règle de calcul Pour calculer la somme des nombres de 1 à 10, on prend la moitié de 10 fois 11, le nombre juste après 10. Ex: 1 + 2 + 3 + … + 100 = ½ x 100 x 101 = 5 050 Formule Vous pouvez utiliser cette formule pour vérifier les sommes indiquées en haut-à gauche.
Solution avec géométrie et algèbre La figure illustre comment calculer la somme des nombres de 1 à 6. Par rapport à la diagonale, on trouve que la quantité de billes vaut: 7² = 2 x (1+2+3+4+5+6) + 7 Formalisons en prenant n au lieu de 6: (n+1)² = 2 x (1+2+3+…+n) + (n+1)
Brèves associées	>>> Somme des entiers – Démonstration avec polynôme générateur
Pour en savoir plus	>>> Nombres entiers >>> Somme des nombres entiers >>> Nombre 666 – Nb de la Bête		>>> Histoire vraie du calcul de Gauss >>> Gauss (1777-1855)

22. Cercle et angles
Triangles inscrits dans le cercle Tous les angles issus d'un point sur le cercle (du même côté) et interceptant le même arc sont égaux, et ils valent la moitié de l'angle centre qui intercepte le même arc.		Triangles avec le diamètre Un triangle avec un diamètre comme côté est toujours rectangle. Normal ! Les angles issus d'un point sur le cercle valent 90° car l'angle correspondant issu du centre vaut le double: 180° (angle plat).
Pour en savoir plus	>>> Cercle >>> Cercle et angles		>>> Angle droit et angle plat >>> Triangle rectangle

23. Algèbre – ax + b
Opération à trous À l'école primaire, nous avons appris à calculer avec les nombres. Au collège, on passe aux calculs avec des symboles qui représentent des nombres pas forcément connus a priori. Algèbre Sans le savoir, les enfants apprennent les concepts de l'algèbre en faisant des opérations à trous. Le carré fait office d'inconnu. En algèbre on convient de le nommer par la lettre x, et, pour ne pas confondre cette lettre avec le signe de la multiplication, on remplace celui-ci par un point. Une fois bien habitué à cette notation, et s'il n'y a pas de risque de confusion, on peut même omettre le point et noter: 2x + 1 = 11		Résolution Vous avez trouvé rapidement que la valeur à mettre dans le carré est 5 car 2 x 5 + 1 = 11. En algèbre, les choses peuvent se compliquer et il est nécessaire de mettre en place des règles qui permettront d'affronter des problèmes plus durs. Le principe reste néanmoins très simple. Imaginez cette expression comme une balance à deux plateaux qui rester en équilibre. Procédure Une seule règle: faire rigoureusement la même opération de chaque côté.
Pour en savoir plus	>>> Algèbre >>> Bases du calcul algébrique		>>> Équations – Débutants >>> Confusion?

24. Nombre 666 – Bête
Apocalypse Le livre de l'Apocalypse mentionne le nombre de la Bête et le donne égal à 666. Ce monstre viendra semer la terreur parmi les hommes et sera anéanti par le retour de Jésus sur la Terre. Il s'agit vraisemblablement de la manière romaine d'exprimer vaguement un grand nombre. Phobie L'hexakosioihexekontahexaphobie, avec 29 lettres, signifie: peur du nombre 666. Ce nombre en grec, se dit: hexakosioï hexekonta hex. Pyramide du Louvre à Paris Elle est recouverte de 666 panneaux en verre de forme losange.		Propriétés mathématiques 666 = 2 x 3² x 37 Formé avec trois 6, c'est un repdigit. Curiosités numériques 666 = 6 + 6 + 6 + 6³ + 6³ + 6³ 666 = (123+132+231+213+312+321) / 2 Curiosité romaine 666 = DCLXVI = (500 + 100 + 50 + 10 + 5 + 1) Tous les symboles romains (sauf M) dans l'ordre décroissant.
Pour en savoir plus	>>> Nombre 666 >>> Nombre de la Bête >>> Repdigit		>>> Chiffre romains >>> Losange

25. Triplets de Pythagore: a² + b² = c²
Recherche de carrés Est-ce qu'il existe des carrés qui sont sommes de deux carrés? Oui! Une infinité. Le plus célèbre: Ces trois nombres sont nommés triplet de Pythagore car cette relation fait penser au théorème de Pythagore. Curiosités numériques		Formation Vous voulez créer des triplets vous-mêmes. Rien de plus facile! Prenez deux nombres u et v; Le premier nombre est a = u² – v²; le deuxième: b = 2uv; et le troisième: c = u² + v² Exemple u = 3 et v = 2 => a = 9 – 4 = 5 b = 2x3x2 = 12 et c = 9 + 4 = 13 En effet: 5² + 12² = 13² Propriétés (quelques) Parmi a, b ou c, l'un est divisible par 5 Parmi a ou b, l'un est divisible par 3 Parmi a ou b, l'un est divisible par 4 Le produit des trois est divisible par 60
Brèves associée	>>> Pythagore – Biographie		>>> Triangles de Pythagore
Pour en savoir plus	>>> Triplets de Pythagore		>>> Pythagore >>> Théorème de Pythagore

26. Belle égalité entre carré et cubes
N'est-ce pas extraordinaire? Tous les nombres jusqu'à 1000, ajoutés et mis au carré donnent un nombre égal à la somme des mêmes nombres au cube: (1 + 2 + 3 + … + 1000)² = 1³ + 2³ + 3³ + … 1000³ Calcul de cette somme La somme des nombres jusqu'à 1000 vaut: (1000 x 1001 ) / 2 = 500 500 Son carré: 250 500 250 000		Belle harmonie entre carrés et cubes En résumé Les mathématiciens formulent cette propriété valable pour tous les nombres n de la manière suivante: On lit: le carré de la somme des nombres k depuis 1 jusqu'à n est égal à la somme des cubes des nombres k depuis 1 jusqu'à n.
Pour en savoir plus	>>> Carré somme de cubes >>> Somme des entiers		>>> Nombre 500 500 >>> Nombre 250 500 250 000

27. Nombres pairs et impairs
En rang par deux. S'il y a un nombre pair d'élèves, ils peuvent tous se mettre exactement en rang par deux. S'il y en a un nombre impair, il reste toujours un élève tout seul. Pour les nombres Pour tous les nombres, on traduit cela très simplement: n est pair si n = 2k (k paires), et n est impair si n = 2k + 1 (k paires + un tout seul). Exemples 100 est pair, car 100 = 2 x 50 101 est impair, car 101 = 2 x 50 + 1 Parité La parité des nombres est utilisée dans de très nombreuses démonstrations de la théorie des nombres. Sa généralisation à la divisibilité par p, un nombre premier, est l'objet d'une branche entière: l'arithmétique modulaire.		Pair et impair Un nombre est pair s'il est divisible par 2 et impair, sinon. Les nombres pairs sont terminés par [0, 2, 4, 6, 8). Les nombres impairs sont terminés par (1, 3, 5, 7, 9). En anglais: pair = even et impair = odd. Deux nombres consécutifs Parmi deux nombres consécutifs, l'un est pair et l'autre impair. Leur somme est impaire et leur produit est pair. Ex: 10 + 11 = 21 = 2 x 10 + 1 10 x 11 = 110 = 2 x 55 Addition et multiplication La somme de deux nombres de même parité est paire (P + P = P et I + I = P). Le produit comportant un nombre pair est pair. Seul le produit de deux nombres impairs reste impair.
Pour en savoir plus	>>> Nombres pairs et impairs >>> Arithmétique des pairs et impairs		>>> Nombre premier >>> Modulo et congruence

28. Dédé …
Jeu de dé De nombreux jeux de société se jouent avec des dés, à commencer par les petits chevaux ou encore le nain jaune. Savez-vous que la somme des points sur deux faces opposées est toujours 7? Les dés sont également source de nombreux exemples de calcul en probabilités. Quelle est la chance d'obtenir un six ou un double-six? Le six En lançant un dé, il peut donner (1, 2, 3, 4, 5 ou 6). Ce qui totalise six cas possibles. Le six étant le cas que nous attendons. On dit que la chance (la probabilité) d'avoir un six est de une sur six. P = 1/6 Combien de lancers pour un six Il ne faut pas croire qu'avec six lancers, le 6 va tomber! Il faut parfois de nombreux lancers avant de le voir arriver. Effectivement la probabilité de 1/6 n'est valable que pour un très grand nombre de lancers. La probabilité tend vers 1/6.		Avec deux dés Quelles sont les possibilités? Si le premier dé montre 1, le second peut donner une des six possibilités de 1 à 6; si le premier montre 2, encore six possibilités pour le second; idem pour la suite. Soit 6 x 6 = 36 possibilités. Le double-six En lançant deux dés, il y a 36 possibilités, mais une seule est dite favorable, celle qui donne 6-6. Au moins un six avec deux dés Compter les cas favorables: si c'est le dé n°1 qui donne le 6; le dé n°2 donne un nombre entre 1et 5. si c'est le dé n°2 qui donne le 6; le dé n°1 donne un nombre entre 1et 5. et, enfin, le cas où les deux donnent 6. Soit 5 + 5 + 1 cas.
Pour en savoir plus	>>> Jeu de dés >>> Jeu de dés et probabilités >>> Jeux et énigmes		>>> Probabilités >>> Loi des grands nombres >>> Jeux de société

29. Taquin – Puzzle 14-15
Le jeu de Taquin Jeu qui se pratique sur un damier de 4 x 4 cases comportant 15 pions numérotés de 1 à 15. Ces pions ne peuvent se déplacer sur le plateau que par glissement dans la seule case vide à un moment donné. Le jeu consiste à remettre les pions dans l'ordre numérique. Invention Sam Loyd (1841-1911), le plus grand faiseur d'énigmes, a créé le jeu de Taquin, un équivalent pour l'époque du cube de Rubic d'aujourd'hui. Le jeu qu'il proposait était le 14-15. Il s'agissait de remettre les pions mobiles dans l'ordre séquentiel correct. Loyd promettait un prix à celui qui y arriverait. Il était, en fait, infaisable … Loyd avait inversé deux pions. Le taquin a mis plusieurs mois avant de connaître la notoriété au fil des publications d'articles dans la presse, comme ce fut le cas du Rubik's Cube. Désormais, avec Internet, la diffusion est instantanée, comme cela s'est passé pour le célèbre et addictif jeu du 2048.		Résolution Dans la mesure où les pions sont correctement disposés sur le plateau, ce puzzle est facile à réaliser. Il constitue néanmoins un bon défi pour les enfants. 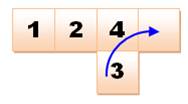Le secret Sur la première ligne, placer le 1 et le 2. Puis, faites monter le 4 dans la position du 3. Mettre le 3 sous le 4 et faites glisser le 4 dans sa position et le 3 dans le trou laissé vaquant. Pour les deux dernières lignes, le même principe s'applique: il faut les construire toutes les deux à la fois.
Pour en savoir plus	>>> Taquin >>> Nombre 15 >>> Rubic's Cube		>>> Jeu du 2048 >>> Jeu de dames >>> Jeu d'échecs

Anglais: Fifteen game / 15-puzzle

Espagnol: Juego del 15

30. Calcul et Maths
Calcul en primaire Le calcul étudié en primaire consiste à maitriser les quatre opérations: addition, soustraction, multiplication et division. Calcul ensuite Que ce soit dans la vie de tous les jours ou pour exercer une profession, le calcul est toujours nécessaire, mais la tâche est grandement facilitée avec l'utilisation des calculateurs et des ordinateurs.		Mathématiques Il n’y a mathématiques que lorsqu’il y a démonstration … Maths au collège Initiation: on peut apprendre, par exemple, que les diagonales des carrés ou des rectangles sont égales, mais sans le démontrer. Démonstrations: apprentissage au collège à partir de la 5^e.
Humour Pensée On fait parfois l'analogie avec la littérature (maths) et l'orthographe (calcul). L'un est le mode opératoire pour pratiquer l'autre. En poussant la comparaison, on note qu'on peut être doué en maths sans être bon en calcul.
Pour en savoir plus	>>> Calcul – Index >>> Mathématiques et ses disciplines >>> Enseignement – Index		>>> Démonstrations >>> Exemple de démonstration >>> Ordinateurs

31. Compter avec dix chiffres
Chiffres et nombres Nous disposons de dix chiffres pour former tous les nombres: 0, 1, 3, 4, 5, 6, 7, 8 et 9. Les chiffres sont plus ou moins "pesants" selon leur position. On dit que nous avons un système décimal de numération de position. Nombres entiers Ce sont les nombres qui servent à compter. Ils ont parfois un petit nom, comme: Une grosse = 12² = 144 Une hécatombe = 100 Une myriade = 10 000 Un googol = 10 suivi de cent zéros		Exemple 3 x 100 + 2 x 10 + 4 = 324 Avec la numération de position, les valeurs en 10 sont sous-entendues. Formation des nombres Un nombre plus à gauche représente un "poids" dix fois supérieur à son voisin de droite: 5 678 = 5 x 1000 + 6 x 100 + 7 x 10 + 8 On lit bien: cinq-mille-six-cent-soixante-dix-huit
Pour en savoir plus	>>> Nombres >>> Chiffres >>> Compter >>> Noms de nombres		>>> Nombres entiers >>> Nombres en toutes lettres >>> Formation des nombres >>> Histoire des nombres

32. Thalès de Milet (625 / 547 av. J.-C.)
		Il est né à Milet en Ionie (ouest de la Turquie actuelle) en 625 ou 640 (?) avant J.-C. L'un des sept sages de la Grèce antique. Le plus ancien mathématicien connu. Marchand, il a fait de nombreux voyages en Crète, en Égypte et en Asie. Il est en fait, le fondateur de la science grecque. Astronome, géomètre, physicien et philosophe. Il fut l’un de ceux qui permirent à l’humanité de passer du stade de l’observation et de l’expérience à celui de la méthode et de la théorie. Il a prévu l'éclipse de Soleil du 28 mai 585. Hérodote raconte que cette prévision mis fin aux combats entre le roi de Babylone Nabuchodonosor et les Lydiens. Les collégiens le connaissent avec son théorème sur la conservation des proportions. Viendront juste après lui: Bouddha, Lao-Tseu ou encore Pythagore. Thalès est une grande société française de défense et de sécurité qui a pris son nom. Il s'agit d'anciennement Thomson-Csf, réunie avec ses nombreuses acquisitions internationales.
Brèves liées	>>> Les grands savants de l'Antiquité – B17
Pour en savoir plus	>>> Thalès >>> Contemporains		>>> Théorème de Thalès

33. Carré magique 3x3
Un carré magique est une grille de chiffres telle que la somme des nombres sur les lignes, les colonnes et les diagonales sont identiques. Pour un carré de trois cases de côtés, ce sont les nombres de 1 à 9 qui sont utilisés. Le carré magique 3x3 est unique, sauf à permuter les nombres. Le nombre central est 5 et la somme de deux nombres opposés est égale à 10. La somme sur toutes les lignes ou sur toutes les colonnes vaut trois fois la somme magique. Or, cette somme est l'addition de tous les nombres de 1 à 9 soit 45. La somme magique est égale à un tiers de celle-ci: 45 / 3 = 15.			6 + 1 + 8 = 15 7 + 5 + 3 = 15 2 + 9 + 4 = 15 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Brèves associées	>>> Carré magique 5x5	>>> Carré alpha-magique
Pour en savoir plus	>>> Carré magique 3x3 >>> Carré latins >>> Somme des entiers successifs	>>> Carré magiques de toutes sortes >>> Sudoku

34. Paradoxe de la corde
Cas général Deux cercles de rayons R et R'. Quelle est la différence de circonférence entre les deux? C'est-à-dire: la différence entre les deux périmètres P et P'. L'écart entre les périmètres est équivalent au périmètre d'un cercle de rayon égal à l'écart des rayons, que les cercles soient petits ou géants. Cas d'une corde autour de l'Équateur Supposons que nous puissions poser une corde sur la ligne d'Équateur. Elle devra mesurer quelque chose comme 40 000 km. On dispose de 6 m de corde en plus. Incroyable! Ce petit ajout permet de soulever la corde de presque 1 m tout autour de la Terre. En effet:			Notations Effet de 6 m de corde en plus, quel que soit le rayon du cercle
Brèves associées	>>> Paradoxe de la corde soulevée	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Paradoxe de la corde >>> Paradoxes	>>> Périmètre du cercle >>> Équateur

35. Bases – Droites dans le triangle
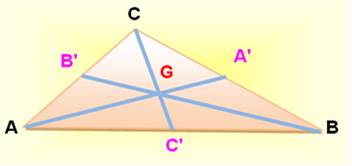
BISSECTRICES Les trois bissectrices sont concourantes au centre du cercle inscrit.		MÉDIANES Les trois médianes sont concourantes au centre de gravité.
HAUTEURS Les trois hauteurs sont concourantes en un point appelé orthocentre.		MÉDIATRICES Les trois médiatrices sont concourantes au centre du cercle circonscrit.
Pour en savoir plus	>>> Droites et points dans le triangle >>> Médianes >>> Médiatrices >>> Hauteurs >>> Bissectrices		>>> Centre de gravité >>> Cercle inscrit >>> Cercle circonscrit

Anglais: Back to basics

36. Factorielles
Jeu de nombres Et si on prenait les nombres les uns après les autres et on les multipliait … Ces nombres sont nommés factorielles et sont notés: 6! = 720. Extraordinaire 40 585 = 4! + 0! + 5! + 8! + 5! Calculette La fonction factorielle est présente sur les calculettes, notamment sur celle de votre ordinateur. On peut jouer à chercher la plus grande valeur calculée avec cet engin. C'est 3 248! = 1,973… 10⁹⁹⁹⁷.			Usage (exemple) Combien de possibilités à un loto de six boules à six chiffres? La première boule est tirée: c'est l'une des 6, soit 6 cas possibles. La deuxième va être tirée parmi les 5 qui restent et c'est 5 cas possibles. La troisième, avec 4 boules, c'est 4 cas. Puis 3 pour la quatrième, 2 pour la cinquième, et finalement, une seule possibilité pour la sixième et dernière. La quantité de possibilités est égale à 6! = 720 Loto français Le calcul complet pour le loto avec 6 boules et 49 numéros plus numéro complémentaire conduit à 19 068 840 possibilités.
Pour en savoir plus	>>> Factorielles >>> Calculette	>>> Factorielles et dénombrements >>> Loto

37. Nombre 2 – DEUX
Propriétés Le nombre 2 est un nombre pair (divisible par 2 sans reste). C'est le plus petit nombre pair et le seul nombre premier pair. C'est la racine carré de 4: C'est la base de la numération binaire. Seul motif du type: 2 + 2 = 2 x 2 Divisibilité Un nombre + son carré est divisible par 2. n² + n = n (n + 1). C'est le produit de deux nombres successifs et l'un d'eux est pair.		Somme 2 + 4 = 6 = 2 x 3 2 + 4 + 6 = 12 = 3 x 4 2 + 4 + 6 + 8 = 20 = 4 x 5 2 + 4 + … + 2n = n (n + 1) Pour n = 200, la somme vaut 100 x 101 = 10 100 Jeu du quatre 4 (ou quatre k) 2 = 1/1 + 1/1; 2 = 2/2 + 2/2; etc.
Brèves liées	>>> Nombre 0 et 1 >>> Nombre 3		>>> Binaire >>> Programmation de la somme
Pour en savoir plus	>>> Nombre 2 – Culture >>> Nombre 2 – Maths		>>> Nombres premiers >>> Jeu du quatre 4

38. Somme des nombres pairs – Programmation
But: calculer la somme des nombres pairs. Programme Scratch Affichage du résultat		Commentaires On a créé deux variables dans l'onglet "Données": Somme et PairMax *Ligne 1:* Instruction qui lance le programme lorsqu'on clique le drapeau vert. *Ligne 2:* Initialisation à 0 de la somme à calculer avant de démarrer les calculs. *Ligne 3:* Initialisation du premier nombre pair à 0. *Ligne 4:* Boucle de répétition des calculs qui figurent entre ces crochets. Les calculs seront effectués tant que PairMax n'aura pas atteint la valeur 200 (valeur à titre d'exemple; on y met le nombre pair que l'on veut). *Ligne 5:* Nous sommes dans le corps de la boucle de répétition. On ajoute 2 à PairMax pour passer au nombre pair suivant à chaque répétition. *Ligne 6:* On ajoute le nouveau nombre pair à la somme. *Bilan:* PairMax va progresser à chaque répétition: 2, 4, 6, 8 … 200 et Somme va prendre les valeurs successives: 2, 6, 12, 20 … 10100. **Astuce: si vous voulez voir la progression, introduisez dans la boucle l'instruction attendre 1 seconde.**
Programme Maple Traduction en français S := 0: pour n de 2 à 200 pas 2 faire S := S + n: fin de faire: S;		Commentaires *Ligne 1:* La somme (S) est initialisée à 0 avant de commencer les calculs. Le symbole indique que l'ordinateur va placer la valeur 0 dans la mémoire nommée S. *Ligne 2:* Le logiciel utilise l'anglais. La deuxième instruction se lit de cette manière: for n from 2 to 200 by 2 do pour n de 2 à 200 par pas de 2 faire Il s'agit d'une boucle qui va répéter le travail autant de fois que nécessaire pour compter de 2 à 200 par pas de 2 (2, 4, 6, …, 198, 200) *Ligne 3:* Le calcul consiste à prendre la valeur actuelle de la somme (S) et lui ajouter n. Au démarrage S = 0 et n = 2; cette instruction va donner une nouvelle valeur à S = 0 + 2 = 2. Au passage suivant dans la boucle, n = 4. Cette valeur est ajoutée à S qui devient 2 + 4 = 6. Etc. *Ligne 4:* Le do anglais (faire) et retourné pour indiquer que c'est la fin de l'écriture de la boucle. *Ligne 5:* S suivi d'un point-virgule indique que la valeur de S doit être montrée à l'écran. **En bleu, justement, la valeur de S, résultat du calcul complet.**
Brèves liées	>>> Nombre 2 – Somme
Pour en savoir plus	>>> Programmation – Index >>> Programmation – Débutant >>> Programmation Scracth		>>> Ordinateur >>> Informatique

39. Nœuds, entrelacs et tresses
Comment les distinguer? NŒUD : une ficelle plus ou moins entortillée et réunies par ses deux extrémités (à gauche). ENTRELACS: deux ou plusieurs ficelles en nœuds (au centre). TRESSE: plusieurs ficelles (brins) plus ou moins nattées dont les extrémités partent toutes d'une zone de départ et aboutissent toutes à une zone d'arrivée, sans revenir en arrière (à droite). Invariant Quantité ou expression algébrique typique d'un nœud. Une aide à leur identification et à leur classification. La quantité de croisements est l'invariant le plus simple. Le trèfle (à gauche) a 3 croisements.		Topologie et nœuds L'étude des nœuds est une branche de la topologie, cette partie des mathématiques qui ne s'intéresse pas aux dimensions, mais seulement aux formes des objets. Dans ce domaine, deux nœuds sont "égaux" (on dit plus exactement "équivalents") si on peut amener l'un sur l'autre par déformation sans rompre la courbe. Tout le problème de la théorie des nœuds est de trouver une méthode pour décider si deux nœuds sont équivalents. Quantité S'il existe un seul nœud avec 3 croisements, de même que pour 4 croisements, on sait qu'il en existe plus d'un million avec 16 croisements. Par contre, on n'a pas encore réussi à les compter pour 17 croisements Cravate En 2014, un mathématicien a recensé 177 147 façons de nouer une cravate.
Pour en savoir plus	>>> Topologie		>>> Nœuds

Retour	Brèves de maths – Page 1
Suite	Brèves de maths – Page 3
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve02.htm

20. Dix en chiffres

21. Somme: 1 + 2 + 3 + 4 + …

22. Cercle et angles

23. Algèbre – ax + b

24. Nombre 666 – Bête

25. Triplets de Pythagore: a² + b² = c²

26. Belle égalité entre carré et cubes

27. Nombres pairs et impairs

28. Dédé …

29. Taquin – Puzzle 14-15

30. Calcul et Maths

31. Compter avec dix chiffres

32. Thalès de Milet (625 / 547 av. J.-C.)

33. Carré magique 3x3

34. Paradoxe de la corde

35. Bases – Droites dans le triangle

36. Factorielles

37. Nombre 2 – DEUX

38. Somme des nombres pairs – Programmation

39. Nœuds, entrelacs et tresses