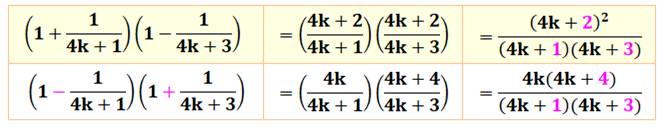|
||||||||||||||||||||||||||||||||||||||||||||
![]()
|
IDENTITÉS DIVERSES Utiles pour la résolution de
certains problèmes. |
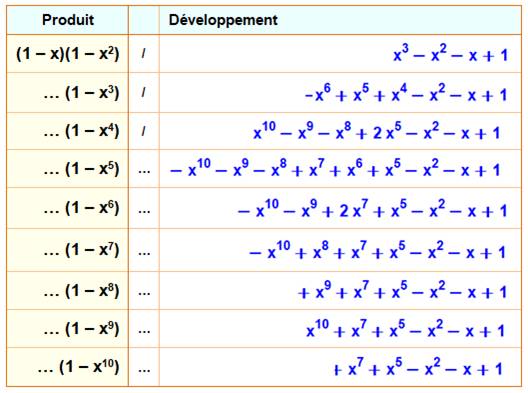
La relation d'Euler avec les nombres
pentagonaux
|
Les exposants sont les nombres
pentagonaux généralisés. Les premiers développements, limités au
degré 10:
Formation progressive des coefficients
Identité reliant un produit à une somme
|
Voir Théorème des nombres pentagonaux
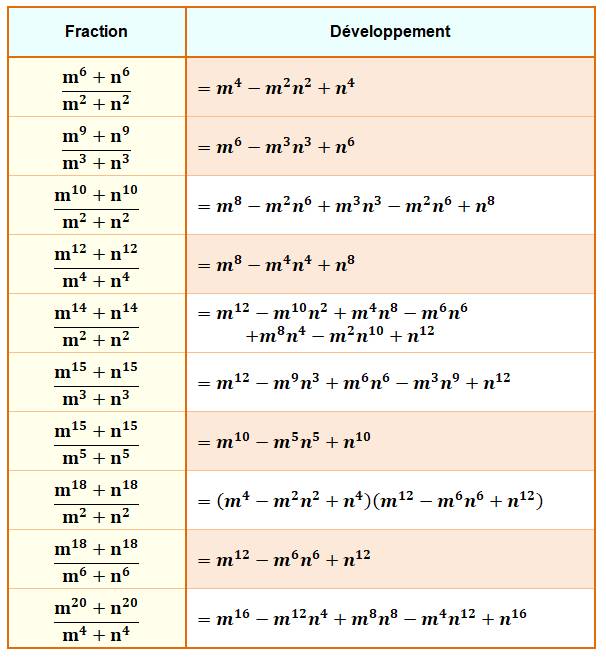
Seules
des fractions développables sans dénominateur sont représentées
|
|
|
|
Les identités en jaune sont utilisées pour
composer des développements
de racine de 2. |
|
|
|
||
|
1 / 2x3 =
1/2 – 1/3 1 / 3x5 = 1/2 (1/3 – 1/5) 1 / 4x7 = 1/3 (1/4 – 1/7) 1 / 5x9 = 1/4 (1/5 – 1/9) … |
|
|
Voir Application
|
|
||
|
1² / 2 =
3/2 = 0 + 1/2 2² / 3 =
4/3 = 1 + 1/3 3² / 4 =
9/4 = 2 + 1/4 4² / 5 = 16/5 = 3 + 1/5 … |
|
|
|
(1 + 1² + 11) / (1x1) = 1 + 1/2 (2 + 2² + 23) / (2x3) = 2 + 1/3 (3 + 3² + 33) / (3x3) = 3 + 1/4 (4 + 4² + 44) / (4x4) = 4 + 1/5 … |
|
|
|
|
||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentDiv.htm
|
![]()