|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PENTAGONE RÉGULIER – Constructions Méthodes approchées, Méthode dite
de Dürer Plusieurs méthodes de construction exactes du
pentagone régulier. Certains
ont cru avoir trouvé d'autres méthodes. Très voisines de l'exactitude, mais
approchée. C'est le cas de la méthode exposée par Albrecht Dürer, sans doute
trouvée avant lui. |
|
|
|||||
|
Construction
rare en architecture médiévale, comparée au triangle
et au carré,
sans doute par méconnaissance de la manière de le construire de façon simple. Méthodes
qui seront connues des architectes à partir du 16e siècle bien que
connues des arts libéraux. Les
maitres-maçons ont plutôt inventé des méthodes d'approximation géométriques. |
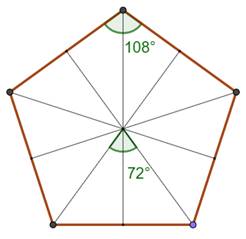
Pourtant le nombre 5 et le pentagone avaient
une valeur hautement symbolique. Nombre 5, symbole des besoins humains, de la
rédemption et de la grâce. Référence aux cinq plaies du Christ (mains, pieds
et flanc droit) ou encore à la parabole des dix vierges
(cinq sages et cinq folles). Nombre cinq de la quintessence
en alchimie: cinquième essence qui assure le cohésion ou la vie, ajoutée aux
quatre premiers: terre, feu, air et eau. Pentagramme
comme symbole de ralliement de l'école de Pythagore. D'autres associent le nombre cinq au dieu ultime
et à la globalité de l'univers. |
||||
|
Construction approchée avec
triangles rectangles (1,3) Tangente (72°) = 3,077… Approximé
à 3 |
|
|
|||
|
|
|||||
|
Méthode approchée dite de Dürer
(1525) Connue du maitre allemand Mathes Roritzer en
1486 (et avant ?) Avantage: une seule ouverture de compas. L'approximation est minime (le vrai pentagone est
en bleu); l'écart est invisible sur la figure complète à droite.
Suite et détails
ci-dessous |
|
||||
Voir Construction avec la
fraction 10/17
|
|
||
|
1486: cette construction figure dans
le Geometria deutsch, manuel de six
feuilles attribué à
l’architecte Matthäus Roritzer
et imprimé à Ratisbonne en 1486. 1525, Dürer a sans doute puisé pour
la présenter dans le tome II de son livre Traité de la mesure, avec la règle
et le compas, en lignes, niveaux et corps entiers (1525) Underweysung der
Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen
corporen La méthode figure dans les manuels
de géométrie sous le nom de méthode Dürer et elle reprise par de nombreux
mathématiciens: Tartaglia, Cardan, Guidobaldo del Monte, Cataldi, etc. 1592, Galilée reprend cette
construction dans son cours de mathématiques. Elle figurait dans les manuels
de Voir Pentagones
fractals de Dürer |
Albrecht Dürer (1471-1528): dessinateur,
graveur et peintre allemand également connu comme théoricien de la géométrie
et de la perspective linéaire. Son livre (1525): Traité de la mesure, avec la règle et le compas,
en lignes, niveaux et corps entiers. Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien,
Ebenen unnd gantzen corporen. Extrait sur la construction du
pentagone
|
|
D'après La géométrie d'Albrechy Dürer
– Jeanne Peiffer
|
|
||
|
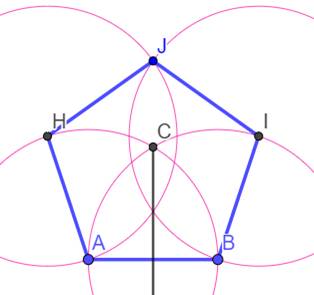
Construction approchée dite de
Dürer Le
segment AB est un côté du pentagone. La même ouverture de compas AB va servir tout le
long de cette construction. Cercle de
centre A et de rayon AB. Cercle de
centre B et de rayon AB. Intersections
en C et D. Cercle
(rose) de centre D et de rayon AB. Intersections
en E, F et G. Droites
EG et FG. Intersections
en H et I. AH et BI
sont deux nouveaux côtés du pentagone. Attention le point G n'est pas sur AB ! Cercle de
centre H et de rayon AB Cercle de
centre I et de rayon AB HJ et IJ
sont les deux derniers côtés du pentagone. Pentagone: ABIJH Pourquoi approchée ? Rayon des cercle = 1 (disons). EF est le diamètre du cercle (D) = 2 Angle EAB = Angle EBF = Droit. Pythagore dans le triangle rectangle EBF: BE = AEF est un triangle rectangle avec côté R et 2R
=> angles
(30°, 60°). Arc AG = Arc GB. EG bissectrice de l'angle AEB. Angle GEB = 15° Loi
des sinus dans le triangle EBI: sin(BEI) / BI = sin(BIE) / BE sin(BIE) = BIE = 26,63387984…° IBE = 180 – 15 – 26, 6… = 138,3661202… Avec ABE = 30° IBA = 138,3… - 30 = 108,3661202 … Au lieu de 108° Erreur relative de 0,34% |
|
|
|
|
||
|
Variante de méthode A1) Triangle
équilatéral ABP. Trois
cercles verts centrés sur les sommets. Intersections
F, G, P et R Droite PR Intersection
Q Droites
FQ et GQ Intersections
E et C Cercles
(E, EA) et (C, CB) Intersection
D Pentagone:
ABCDE. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir les liens en première page
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PentaCo3.htm
|
![]()