NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Calculs avancés
Débutants Multiplication	MULTIPLICATION			Glossaire Multiplication
INDEX Calcul Opérations	TABLES	Tables vues autrement	Terminaisons
	Calcul autour de 10	Calcul deux chiffres	Abaque / Boulier
	Musulmane et...	Védiques	Avec les doigts
	Décimales	Produits	Visuelles
			Grands nombres
		Sommaire de cette page >>> Multiplication géométrique >>> Calcul des unités >>> Calcul des dizaines >>> Bilan >>> Chiffres des unités de la multiplication

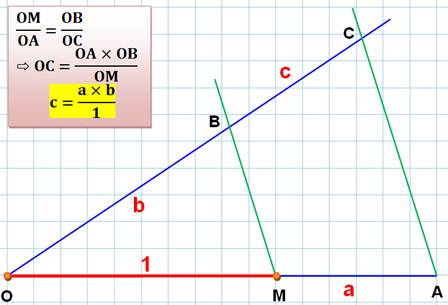
MULTIPLICATIONS VISUELLES

Méthode originale de présenter les tables de multiplication. Elle consiste à trouver d'abord les unités puis les dizaines en s'aidant d'un graphique.

Méthode imaginée par M. Guérin, légèrement revisitée.

Multiplication géométrique
Un segment OM de longueur unité. Sur lui, on pose un segment OA de longueur a. Sur une sécante quelconque en O, on pose le segment OB de longueur b. On trace MB et sa parallèle AC. La mesure du segment AC est égale au produit: c = a . b. Cette propriété résulte de l'application du théorème de Thalès.

Méthode Guérin (Pour les curieux)

Calculs des unités
Ici repose toute l'originalité de la méthode. Les unités à trouver sont présentées dans un tableau de 3 x 3. Multiplicateur (A) et multiplicande (B) sont utilisés pour parcourir le tableau.
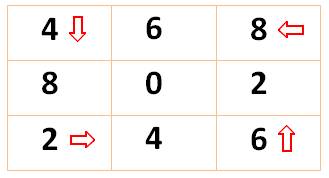
Le multiplicateur est Impair (sauf 5) Exemple 1: Je multiplie 7 par 3. Je pars du 7 Je progresse vers le bas de 3 cases Le résultat est 1. Exemple 2, illustrant la progression: Je multiplie 7 par 7. Je pars du 7 Je progresse vers le bas de 7 cases: 7, 4, 1, 8, 5, 2, 9. Le résultat est 9.	Départ en A (impair) et progression de B cases selon la direction indiquée.
Le multiplicateur est pair Exemple 1: Je multiplie 4 par 3. Je pars du 4 Je progresse vers le bas de 3 cases L'unité est 2. Exemple 2, illustrant la progression: Je multiplie 4 par 7. Je pars du 4 Je progresse vers le bas de 7 cases: 4, 8, 2, 6, 0, 4, 8. L'unité est 8.	Départ en A (pair) et progression de B cases selon la direction indiquée.
Le multiplicateur est égal à 5	Si le multiplicande est impair l'unité est 5; s'il est pair, l'unité est 0.

Calculs des dizaines
Avec le tableau sous les yeux, il suffit de compter les pions rouges. Exemple 1: Je multiplie 4 par 3. Sur la ligne 4 (A = 4), je compte la quantité de pions rouges Pour avancer de 3 cases (B = 3), j'en compte 1 seul. La dizaine est 1. Exemple 2: Je multiplie 9 par 7. Sur la ligne 9 (A = 9), je compte la quantité de pions rouges Pour avancer de 7 cases (B = 7), j'en compte 6. La dizaine est 6.

Bilan

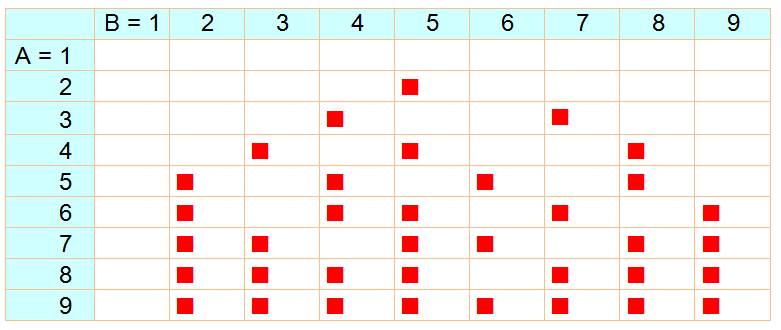
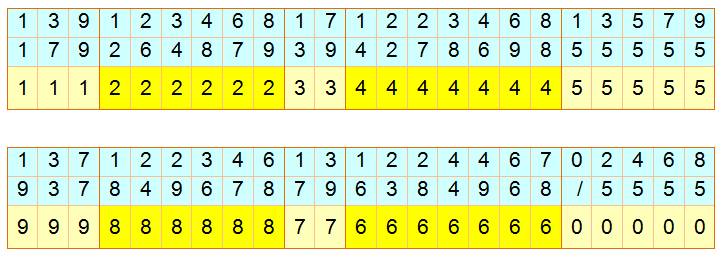
La méthode est très simple à condition de disposer des graphiques.

Notez que la présence des pions rouges témoigne simplement d'un changement de dizaine. On aurait pu indiquer directement la dizaine à trouver dans le tableau à double-entrée.

La méthode originelle de M. Guérin reprend les grilles 3 x 3 pour montrer le calcul des dizaines. Simple variante graphique.

Pour mémoire chiffres des unités
Quelles sont les multiplications qui donnent telle ou telle unité?

Suite	Voir en tête Multiplication Multiplication - Glossaire Multiplications amusantes Multiplications magiques Multiplications pannumériques
Voir	Base décimale Calcul des carrés Calcul mental Calcul védique Initiation aux opérations Preuve - Glossaire Puissance de 10 Puissances - Index Tables de multiplication Théorie des nombres Unités et dizaines
DicoNombre	Nombre 5 Nombre 6 Nombre 7 Nombre 8 Nombre 9 Nombre 11 Nombre 12
Site	Multiplication visuelle selon la méthode Guérin
Cette page	http://villemin.gerard.free.fr/Calcul/MultiGra.htm