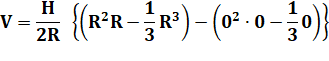Prisme traversant un cylindre, volume

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/03/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OBJETS 3D
Débutants Géométrie	VOLUMES					Glossaire Géométrie
INDEX Cylindre Géométrie	Cube	Sphère		Cylindre		Cône
	Pavé	Cylindre – Exercices			Fourmi sur cylindre
	Rond de serviette		Aire maximale		Cylindre et prisme
		Sommaire de cette page >>> Cas simple du pavé dans le cylindre >>> Cas simple du prisme de la taille du cylindre >>> Géométrie du problème >>> Calcul ave tableur >>> Calcul par intégrale

CYLINDRE traversé par un PRISME

Calcul du volume de la partie du prisme intérieure au cylindre.

Nous cherchons le volume de ce solide:

Ca pratique avec R = 8,5 et angle du prisme 15°.

On calcule des ordres de grandeurs avant le calcul final

Cas simple du pavé dans le cylindre
Un cylindre droit circulaire est traversé par un pavé droit (parallélépipède) perpendiculairement à son axe. La forme découpée est un petit cylindre droit de même diamètre. Quel est le volume de ce petit cylindre en fonction de h, et en fonction de l'angle alpha ? La section diamétrale est la coupe par un plan vertical passant par un diamètre du cylindre.
Volume du cylindre intersecté:
Volume en fonction de l'angle
Application au quart de cylindre	tan(a) = tan(15°) = 0,26795 H = 8,5 x 0,26795 = 2,27757 V = 3,14 x 8,5³ x 0,2679 / 4 = 129,241
Taille du cône, moitié du cylindre	V = 130 / 2 = 65

Cas simple du prisme de la taille du cylindre
Prisme d'angle a = 15° et base R x R = 8,5²
Volume du prisme
Application au quart de cylindre	V = 8,5² x 2,277 / 2 = 82,2771

Ce que nous cherchons

Le volume du prisme complet sera inférieur à ces deux volumes calculés: 130 et 82

Il sera même inférieur au volume du cône: 65.

Nous avons calculé le quart du volume complet car plus pratique pour la suite.

Nous allons utiliser deux méthodes: le tableur pour une sommation discrètes de volumes et une méthode plus précise par calcul d'intégrale.

Géométrie du problème
La section diamétrale est utilisée comme référence (triangle bleu du haut). On forme une tranche du volume cherché en faisant une section parallèle à celle de référence, à la distance x du centre du cercle et d'une épaisseur dx. Le volume cherché est la somme de toutes ces mini-tranches pour toutes les valeurs successives de x avec un pas égal à dx.
Hauteur
Taille du petit rayon
Taille de la petite hauteur: les triangles bleus sont semblables
Volume de la tranche
Volume du quart du solide cherché

Calcul sur Tableur

Exemple de réalisation

En tête les paramètres de calcul

Quantité de pas de calcul: 100

Rayon du cylindre: 17/2 = 8,5

Angle a de 15% et sa tangente: 0,2679…

Hauteur calculée du prisme: H = 2, 277…

Pas de calcul: dx = R/100 = 0,085

Ensuite, les lignes de calcul pour chaque pas noté i, avec dans l'ordre

valeur de la distance au centre x = 8,5/100 i

valeur du petit rayon r = racine (R² - x² )

valeur de la petite hauteur h = H/R . r

volume de la tranche v = ½ r . h . dx

Fin de tableau

Après le dernier pas, le centième, calcul de la somme de toute la colonne en v

et multiplication par 4 pour avoir le volume du solide cherché complet.

Un calcul avec 1000 pas donne:

4V = 219,567

Vraisemblance

Le résultat est bien proche mais inférieur au 65 du cône.

…

Calcul par intégrale
Intégrale
Primitive Chaque monôme passe au degré supérieur et le coefficient est l'inverse de l'exposant. On se souvent que dans l'autre sens, la dérivée de 1/3 x³ = 1/3 x 3 x² = x²
Intégration par partie: Différence entre valeur pour x = R et pour x = 0.
Application numérique	V = 54,85143259 … 4V = 219,4057304 …