|
||||||||||||||||||||||||||||||||
![]()
|
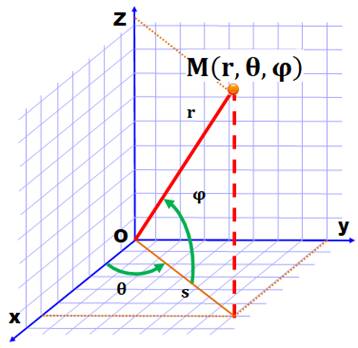
SPHÈRE – AIRE et VOLUME Calcul par intégrales
Pour
le calcul du volume de la sphère, les mathématiciens
de l'Antiquité procédaient par approximations. Les modernes ont inventé un
outil puissant et rigoureux: le calcul intégral. |
|||||||||
|
|
||
|
Principe Calculer
le volume de la sphère en faisant la somme
des volumes des disques jaunes, considérés comme aussi fins que l'on veut. Calculs |
|
|
|
Volume du disque jaune (cylindre): |
|
|
|
Volume de la sphère: passage d'une somme discrète
(sigma) à une somme continue (intégrale): |
|
|
|
|
||
|
Retour au volume avec quelques aménagements: |
|
|
|
Primitive
de y = x² + c => x3/3
+ cx + cste |
|
|
|
Intégration par parties (différence des
primitives entre les deux bornes): |
|
|
|
Finalement: |
|
|
Voir Calcul géométrique
|
|
||
|
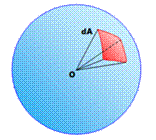
Principe Calculer
l'aire de la sphère en faisant la somme
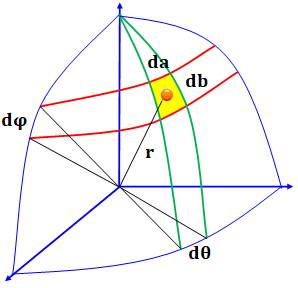
des surfaces élémentaires, considérées comme aussi petites que l'on veut. La
surface élémentaire dA est limitée par un angle infinitésimal ( L'aire de
la sphère est la somme de toutes ces surfaces infinitésimales. |
|
|
|
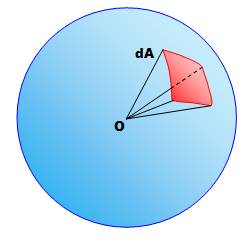
Coordonnées polaires Un point M sur la sphère est repéré par trois
paramètres:
Coordonnées cartésiennes (pour
info)
La longueur
d'un arc est égale au rayon multiplié par l'angle exprimé en radians. Pour db, sur le grand cercle en Phi:
Pour da, sur le petit cercle de rayon r∙cos(phi),
cercle de latitude: Surface élémentaire
Surface complète de la sphère Faire pivoter la surface élémentaire en:
|
|
|
|
Calcul de la surface par
intégration Somme des dA sur toute la sphère: Et, avec séparation des éléments indépendants: |
|
|
|
Primitive Primitive
du cosinus: le sinus. Pour thêta, la primitive d'un élément d'angle,
c'est l'angle lui-même. |
|
|
|
Intégration par parties (différence des valeurs
entre les deux bornes): |
|
|
|
Soit finalement, l'aire de la sphère: |
|
|
|
Volume On intègre l'aire selon le rayon de 0 à r: |
|
|
|
Calcul avec primitive de x2 = x3 /
3: |
|
|
|
|
|||
|
Pour une
courbe paramétrée avec x() et y(t), la longueur d'un arc est: |
|
||
|
Par une
rotation autour de x, aire de la surface obtenue: |
|
||
|
Si la
courbe est un cercle: |
x(t) = r cos(t) et y = r sin(t)
pour t de 0 à Pi |
||
|
En
remplaçant: |
|
||
|
Intégration |
|
||
Merci à JMJ pour sa relecture attentive et ses conseils
![]()
|
Suite sur la sphère |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()