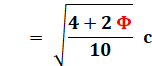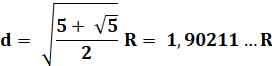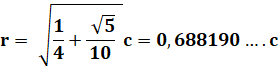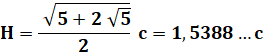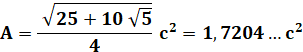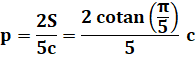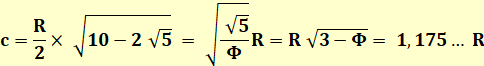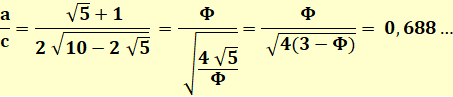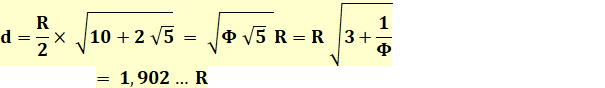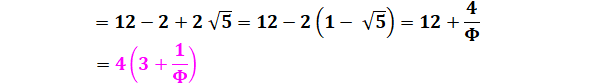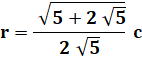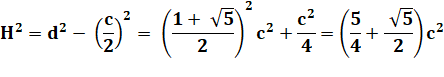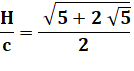|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Accès aux autres polygones
![]()
|
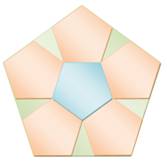
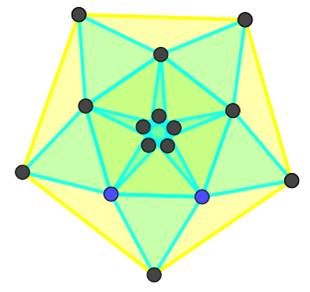
PENTAGONE RÉGULIER sous toutes les coutures Toutes les
mesures du pentagone régulier convexe. Notez la propriété fondamentale de ses
diagonales: longueur égale au nombre d'or
et découpe des diagonales en inverse du nombre d'or (Illustration
ci-dessous). |
Angles du pentagone régulier
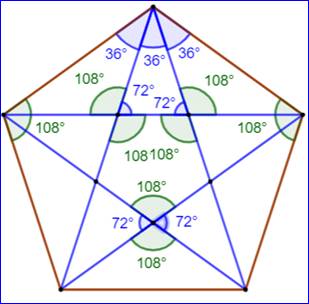

Voir Approximation de la
tangente de 72° / du sinus de 36° / Énigmes
avec les angles
Diagonales et leur découpe en nombre d'or /
Pentagones gigognes
Sachant que
de base: diagonale / côté = nombre d'or (phi)


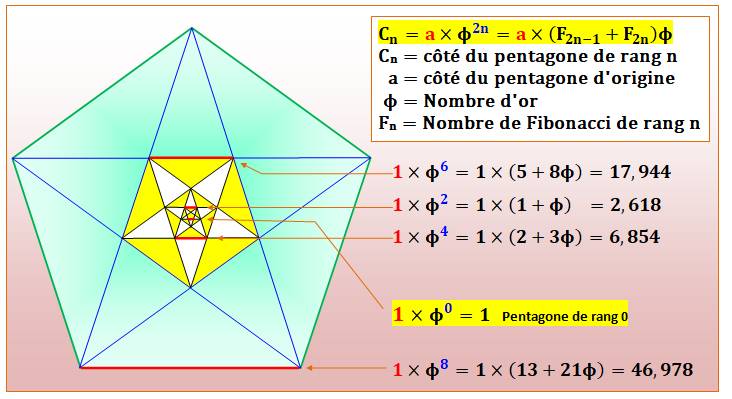
Voir Puissances
du nombre d'or Phi (Phi² = Phi + 1) / Nombres de
Fibonacci
Merci à Bruno Capelle pour l'idée de mettre en valeur les
relations métriques dans cette figure gigogne
|
|
|||
|
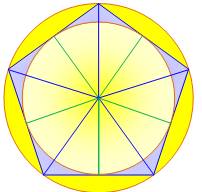
Les deux triangles colorés sur la figure sont
importants car ils permettent le calcul des longueurs des divers segments
inclus dans le pentagone régulier. Ci-dessous, les principaux éléments de calcul. |
|
||
|
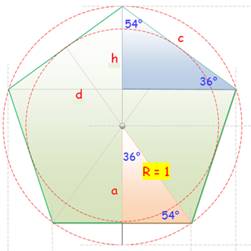
Dans le pentagone, on trouve deux triangles
rectangles 36 – 54. Ils sont assemblés par un côté de l'angle droit pour
former deux triangles isocèles (voir figure
ci-dessous). La dimension de référence est l'hypoténuse de l'un
d'eux: R = 1, le rayon du cercle
circonscrit du pentagone. Ce triangle (celui du bas sur le dessin du
pentagone complet) est répété dix fois pour couvrir complètement le
pentagone. On passe de l'un à l'autre en prenant le côté c/2
pour former l'hypoténuse c de l'autre triangle. Notez bien qu'ils sont de
tailles différentes. |
|
||
Voir Triangles rectangles typiques
/ Angles du pentagone
|
|
||||||||||||||||
|
Formules principales
connaissant la longueur du côté (c)
Pour relations avec nombre d'or, voir notes de calcul. Voir Calcul de la
hauteur H selon deux méthodes / Nombre
3,618… Relations illustrées
pour R = 1
Relations croisées
pour c = 1 ou R = 1 ou r = 1
|
||||||||||||||||
Pentagone unité en coordonnées cartésiennes

|
|
||
|
L'apothème p est aussi le rayon
du cercle inscrit au pentagone. Si S est
l'aire du pentagone, c'est aussi l'aire des cinq triangles du type OAB dont
l'aire vaut: ½ p·c On en
déduit la longueur de l'apothème:
|
|
|
Voir Apothème du décagone / Brève
912
|
Formules
développées en racine de 5 et avec le nombre d'or
a = 1,618/2 = 0,809…
Merci à Jean-Louis Beuil pour ses précisions Notes de calcul
pour mise en évidence du nombre d'or:
A = 5/2 a.c Exemples: Si c = 16 alors a = 11, 011… et A = 440, 442… Si c = 1
alors a = 0, 688… et A = 1, 720… Si c = 10 alors a = 6, 882… et A = 172,047…
|
Voir Angles et
trigonométrie dans le pentagone / Aire
du pentagone / Autres
mesures dans l'étoile / Apothème
|
|
|||
|
La
hauteur est la perpendiculaire à un côté issue du sommet opposé. Elle est égale à la somme
des rayons des cercles inscrit et circonscrit. |
|||
|
|
|
||
|
Avec la diagonale et le théorème
de Pythagore |
|
||
|
Méthode 2 Avec les rayons : H = R + r Ici, le calcul avec
les radicaux est difficile; on passe aux carrés. "On enlève
le chapeau le temps des calculs et on le remet à la fin". |
|
||
|
|
|
|
Comment partager un pentagone
régulier en quatre triangles
isocèles et former un trapèze
isocèle avec ces quatre pièces. Solution
Formulation et application numérique
|
|
|
|
||
|
Figure
formées avec un pentagone et les triangles équilatéraux intérieurs et
extérieurs tracés sur les côtés. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Pentagon.htm |
![]()