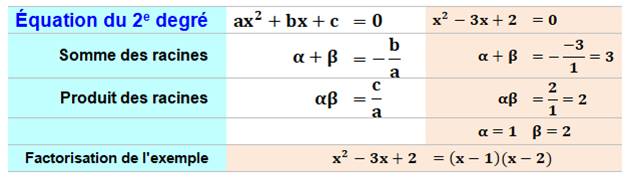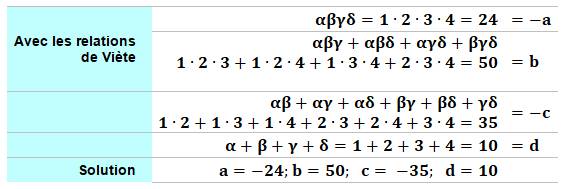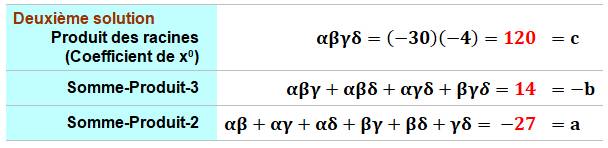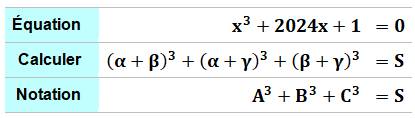Relations de Viète entre racines

Édition du: 18/12/2023

INDEX Équations Algèbre	Équations
	Généralités	Techniques de base	Diophantienne
	Premier degré	Deuxième degré	Troisième degré
	Deux inconnues	Deux équations ou plus	Déterminant
	Inéquation	Avec exposant	Réduction
		Relations de Viète

Faites un double-clic pour un retour en haut de page

Relations de Viète

liant les racines aux coefficients

Les relations de Viète (1540-1603) expriment les relations intimes entre les racines d'une équation et les coefficients du polynôme. Relations prouvées par Viète en 1579.

Illustration: exemple avec le troisième degré

Sommaire de cette page

>>> Cas du deuxième degré

>>> Cas du troisième degré

>>> Cas du quatrième degré

>>> Cas général

>>> Énigme – Exemple d'application

Débutants

Équations

Glossaire

Équations

Anglais: Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots.

Cas du deuxième degré		haut
Deuxième degré Pour l'équation du second degré on sait que les coefficients représentent la somme et le produit des racines. On nomme S la somme et P le produit; les deux racines sont nommées α et β. Les coefficients du polynôme sont b et c. Si le coefficient de a n'est pas l'unité (ni nul), il suffit de diviser tous les termes du polynôme par a.	Formulations équivalentes x² + bx + c = 0 x² – Sx + P = 0 x² – (α+β) + αβ = 0 (x – α) (x – β) = 0 Coefficient de tête ax² + bx + c = 0 x² + (b/a) x + (c/a) = 0
Relations de Viète et exemple numérique Connaissant la somme et le produit, il n'est pas très difficile de trouver les deux racines.

Cas du troisième degré

haut

Relations de Viète et exemple numérique

Avec ces trois relations entre les racines, pas si évident de trouver les trois racines.

Ici, on peut deviner que 6 = 1 × 2 × 3 et tester les autres relations.

Cas du quatrième degré

haut

Relations de Viète et exemple numérique

Avec ces quatre relations entre les racines, pas si évident de trouver les quatre racines.

Ici, on peut deviner que 24 = 4! = 1 × 2 × 3 × 4 et tester les autres relations

Cas général

haut

Relations de Viète et exemple numérique

Applications

La somme et le produit des racines d'un polynôme quadratique P sont 9 et 20. Par ailleurs, le polynôme vaut 4 pour x = 6.

Retrouver le polynôme.

Avec les relations de Viète: P(x) = a(x² – 9x + 20)

Avec la valeur en 6: P(6) = a(36 – 54 + 20) = 2a = 4 => a = 2

Solution: 2x² – 18x + 40.

On donne a – a² + 1 = 0 et b – b² + 1 = 0 avec a différent e b.

Évaluer a + b + ab.

Les deux relations données impliquent que a et b sont deux racines distinctes de x² – x – 1 = 0

Viète nous dit: a + b = 1 et ab = –1

Alors: a + b + ab = 1 + (-1) = 0

Quelles sont les racines de x² + px + q = 0, sachant que p + q = 198 ?

Relations de Viète: α + β = -p et αβ = q

Alors: p + q = 198 = αβ – (α + β)

Factorisation: (α – 1)( β – 1) = 198 + 1 = 199

Or 199 est premier: 199 = 1 × 199.

Deux solutions: {200, 2} et {0, –198 }.

Un polynôme du troisième degré avec:
α + β + γ = 10; αβ + αγ + βγ = -1 et αβ = -6

Quel est le polynôme ?

Avec Viète, la solution se lit immédiatement

x³ – 10x² – x + 6 = 0

Avec x² – 3x + 2 = 0, trouver la valeur de α² + β².

α² + β² = (α + β)² – 2αβ = 3² – 2×2 = 5

En fait les racines sont: 2 et 1 et le polynôme s'écrit: (x – 2) (x – 1).

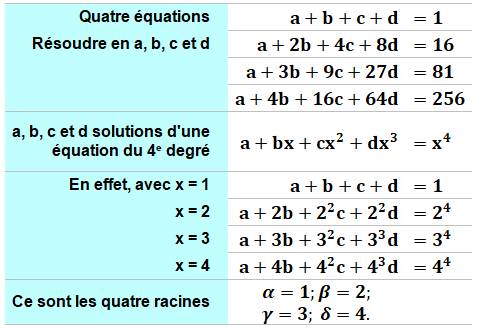
Exemple d'application 1 (4^e degré)		haut
Énigme Résoudre ce système d'équations. Piste On observe que chaque équation a pour coefficients successifs les puissances croissantes du coefficient de b. Les quatre inconnues a, b, c et d peuvent être représentées par un polynôme générique du quatrième degré dont on devra trouver les coefficients.
Polynôme du quatrième degré et ses racines Application des relations de Viète Allure du graphe Les racines en 1, 2, 3 et 4 sont bien visibles en y = 0 (sur l'axe des x).

Voir Défis en algèbre

Exemple d'application 2 (4^e degré)		haut
Énigme Les racines de ce polynôme sont en progression arithmétique. Quelle est la valeur de q ?
Piste Le coefficient de x³ est nul. La relation de Viète nous dit qu'alors la somme des racines est nulle. Étant en progression arithmétique, les quatre racines sont symétriques (sinon la somme serait positive, non nulle). La progression arithmétique est égale à (x) – (– x) = 2x. Valeur à appliquer à y pour étendre la progression.	Allure des racines -y, -x, x, y Raison de la progression: 2x -3x, -x, x, 3x
Poursuite du calcul avec les relations de Viète Racines Sachant que x² = 4 => Racines = { –6, –2, 2, 6}.

Exemple d'application 3 (4^e degré)		haut
Problème Une équation du quatrième degré dont on connait trois des quatre racines: 2, -3 et 5. Restituer les coefficients a, b et c.
Piste Le coefficient de x³ est nul, ce qui veut dire que la somme des racines est nulle. Connaissant les trois autres, la quatrième est facilement déductible. Notez que peut importe le nom, les racines sont interchangeables.
Deux solutions pour trouver les coefficients

Exemple d'application 4 (3^e degré)			haut
Problème Une équation du troisième degré. Calculer la somme S des cubes des sommes des racines deux à deux.
Pour commencer Résumé de l'énoncé et notation On note que la somme des racines est nulle (pas de coefficients pour x²). On note aussi que leur produit vaut -1.
Calculs Voir Identité de Gauss avec a³ + b³ + c³ Note Le coefficient de x est totalement neutre. Il est déroutant d'y mentionner l'année en cours. La somme 3 est inattendue, car l'expression de chacune des racines n'est pas simple. Exemple pour la racine réelle (les deux autres sont complexes): Les trois racines et la somme demandée

Haut de page (ou double-clic)

Suite	Équation – Glossaire et index Techniques de base Exercices simples Réduction des termes d'une équation Équations énigmatiques – Index Voir haut de page
Voir	Algorithme d'Héron Équation avec racines carrés Équation de Pell Équation en x⁴ par factorisation Équations diophantiennes Inéquations Les 17 équations qui ont changé le monde Méthode de Newton Puissance quatrième Structure algébriques et équations
Sites	Relations entre coefficients et racines – Wikipédia La formule de Viète sur les polynômes – mathweb.fr Vieta's Formula – Geesforgeek Vieta's Formula – Wolfram MathWorld Application of Vieta's Formula – Learn math daily Application of vieta’s theorem – Slideshare Vieta's Formula: a simple example – Chan Lye Lee
Cette page	http://villemin.gerard.free.fr/ThNbDemo/VieteRel.htm