|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES
MULTI PUISSANTES Il
s'agit d'une égalité qui reste vérifiée même en changeant la puissance de tous
ses termes. Le jeu consiste à trouver le plus de valeurs de la puissance tout
en conservant l'égalité de départ. Les mathématiciens Euler et Goldbach s'adonnèrent à ces recherches
et mirent au point des équations permettant de les calculer. |
|
Pour une
nomenclature de tous les problèmes posés par les sommes de puissances Voir S'y retrouver |
|
|
|
|
Exemple p = 1 1
+ 8 + 8 = 2
+ 5 + 10 =
17 p = 2 1²
+ 8² + 8² = 2² + 5² + 10² = 129
Que n = p ou à plus ou moins 1 près,
etc. |
|
|
|
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
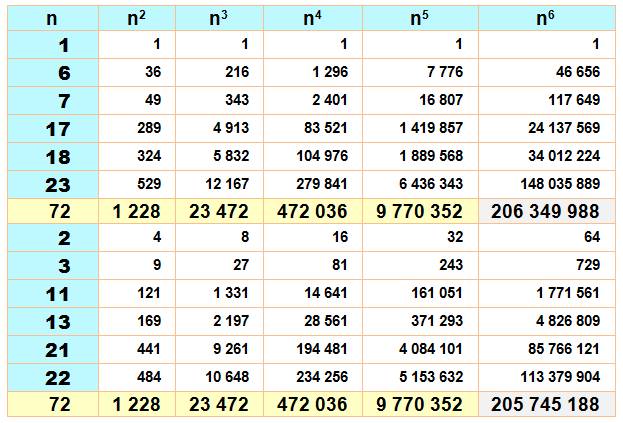
Quatre termes dans l'égalité
et vraie pour les puissances 1 à 3 Somme magique sur le
carré incliné (pointillés bleus) 5 + 3 +
12 + 14 = 2 + 8 + 15 + 9 = 34 Les carrés 52
+ 32 + 122 + 142 = 22 + 82
+ 152 + 92 = 342 = 374 Les cubes 53
+ 33 + 123 + 143 = 23 + 83
+ 153 + 93 = 343 = 4 624 Six termes dans l'égalité et
vraie pour les puissances 1 à 5
|
|
|
|
||
|
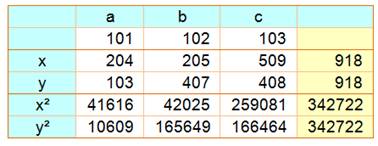
Soit trois entiers a, b et c, il existe une
infinité d'égalités du type: x1 + x2 + x3
= y1 + y2 + y3 |
Équations x1 = a + c x2 = b + c x3 =
2a + 2b + c y1 = c y2 =
2a + b + c y3 = a
+ 2b c Exemple
|
|
|
Summum avec huit égalités
magiques |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Huit sommes
égales à 1 665 132 + 654 + 879 = 231 + 456 + 978 = 174 + 639
+ 852 = 258 + 471 + 936 = 159 + 672
+ 834 = 276 + 438 + 951 = 294 + 618
+ 753 = 357 + 492 + 816 = 1 665
Les égalités sont
résistantes aux quinze permutations
de 1 à 3 chiffres (le premier tableau les montre toutes). Les huit sommes
originales deviennent 8 x 6 = 48 égalités avec la permutation des trois chiffres
de chaque nombre. Les égalités sont
également vérifiées pour le carré
des nombres dans les quinze permutations (somme en colonne de droite). Deux
sommes développées avec leurs quinze égalités avec permutations
Les six
autres mêmes sommes (= 1 665)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
pour une nomenclature des sommes de puissances |
|
|
Puissance |
|
|
|||
|
|
Nombre de termes |
||||
|
|
" |
|
|||
|
Nombre d'égalités
(rien si 1) |
|||||
|
|
|||||
|
p |
n |
n |
p |
N = a1p
+…+ anp avec p = 1 à q |
|
|
p |
p |
p |
p |
|
|
|
p |
p +1 |
p + 1 |
p |
|
|
|
|
|
|
|
Voir aussi |
|
Voir Suites et
exemples
![]()
Table des égalités pour les entiers et
les carrés jusqu'à une somme d'entiers égale à 30
|
a |
b |
c |
d |
aa |
bb |
cc |
dd |
S1 |
S2 |
|
1 |
5 |
6 |
|
2 |
3 |
7 |
|
12 |
62 |
|
2 |
6 |
7 |
|
3 |
4 |
8 |
|
15 |
89 |
|
1 |
6 |
8 |
|
2 |
4 |
9 |
|
15 |
101 |
|
1 |
4 |
6 |
7 |
2 |
3 |
5 |
8 |
18 |
102 |
|
3 |
7 |
8 |
|
4 |
5 |
9 |
|
18 |
122 |
|
2 |
7 |
9 |
|
3 |
5 |
10 |
|
18 |
134 |
|
1 |
8 |
9 |
|
3 |
4 |
11 |
|
18 |
146 |
|
1 |
7 |
10 |
|
2 |
5 |
11 |
|
18 |
150 |
|
1 |
4 |
7 |
8 |
2 |
3 |
6 |
9 |
20 |
130 |
|
1 |
7 |
12 |
|
3 |
4 |
13 |
|
20 |
194 |
|
4 |
8 |
9 |
|
5 |
6 |
10 |
|
21 |
161 |
|
3 |
8 |
10 |
|
4 |
6 |
11 |
|
21 |
173 |
|
2 |
9 |
10 |
|
4 |
5 |
12 |
|
21 |
185 |
|
2 |
8 |
11 |
|
3 |
6 |
12 |
|
21 |
189 |
|
1 |
9 |
11 |
|
3 |
5 |
13 |
|
21 |
203 |
|
1 |
8 |
12 |
|
2 |
6 |
13 |
|
21 |
209 |
|
2 |
5 |
7 |
8 |
3 |
4 |
6 |
9 |
22 |
142 |
|
1 |
6 |
7 |
8 |
3 |
4 |
5 |
10 |
22 |
150 |
|
1 |
5 |
7 |
9 |
2 |
4 |
6 |
10 |
22 |
156 |
|
1 |
4 |
8 |
9 |
2 |
3 |
7 |
10 |
22 |
162 |
|
1 |
10 |
11 |
|
2 |
7 |
13 |
|
22 |
222 |
|
2 |
8 |
13 |
|
4 |
5 |
14 |
|
23 |
237 |
|
2 |
5 |
8 |
9 |
3 |
4 |
7 |
10 |
24 |
174 |
|
1 |
5 |
8 |
10 |
2 |
4 |
7 |
11 |
24 |
190 |
|
1 |
4 |
9 |
10 |
2 |
3 |
8 |
11 |
24 |
198 |
|
5 |
9 |
10 |
|
6 |
7 |
11 |
|
24 |
206 |
|
4 |
9 |
11 |
|
5 |
7 |
12 |
|
24 |
218 |
|
3 |
10 |
11 |
|
5 |
6 |
13 |
|
24 |
230 |
|
3 |
9 |
12 |
|
4 |
7 |
13 |
|
24 |
234 |
|
2 |
10 |
12 |
|
4 |
6 |
14 |
|
24 |
248 |
|
2 |
9 |
13 |
|
3 |
7 |
14 |
|
24 |
254 |
|
1 |
11 |
12 |
|
4 |
5 |
15 |
|
24 |
266 |
|
1 |
10 |
13 |
|
3 |
6 |
15 |
|
24 |
270 |
|
1 |
9 |
14 |
|
2 |
7 |
15 |
|
24 |
278 |
|
2 |
7 |
15 |
|
1 |
9 |
14 |
|
24 |
278 |
|
1 |
8 |
15 |
|
3 |
5 |
16 |
|
24 |
290 |
|
2 |
11 |
12 |
|
3 |
8 |
14 |
|
25 |
269 |
|
1 |
10 |
14 |
|
4 |
5 |
16 |
|
25 |
297 |
|
3 |
6 |
8 |
9 |
4 |
5 |
7 |
10 |
26 |
190 |
|
2 |
7 |
8 |
9 |
4 |
5 |
6 |
11 |
26 |
198 |
|
2 |
6 |
8 |
10 |
3 |
5 |
7 |
11 |
26 |
204 |
|
2 |
5 |
9 |
10 |
3 |
4 |
8 |
11 |
26 |
210 |
|
1 |
7 |
8 |
10 |
3 |
5 |
6 |
12 |
26 |
214 |
|
1 |
6 |
9 |
10 |
3 |
4 |
7 |
12 |
26 |
218 |
|
1 |
6 |
8 |
11 |
2 |
5 |
7 |
12 |
26 |
222 |
|
1 |
5 |
9 |
11 |
2 |
4 |
8 |
12 |
26 |
228 |
|
1 |
5 |
8 |
12 |
2 |
3 |
10 |
11 |
26 |
234 |
|
1 |
4 |
10 |
11 |
2 |
3 |
9 |
12 |
26 |
238 |
|
1 |
3 |
8 |
14 |
2 |
4 |
5 |
15 |
26 |
270 |
|
3 |
9 |
14 |
|
5 |
6 |
15 |
|
26 |
286 |
|
1 |
12 |
13 |
|
3 |
7 |
16 |
|
26 |
314 |
|
6 |
10 |
11 |
|
7 |
8 |
12 |
|
27 |
257 |
|
1 |
4 |
10 |
12 |
2 |
5 |
6 |
14 |
27 |
261 |
|
5 |
10 |
12 |
|
6 |
8 |
13 |
|
27 |
269 |
|
4 |
11 |
12 |
|
6 |
7 |
14 |
|
27 |
281 |
|
4 |
10 |
13 |
|
5 |
8 |
14 |
|
27 |
285 |
|
3 |
11 |
13 |
|
5 |
7 |
15 |
|
27 |
299 |
|
3 |
10 |
14 |
|
4 |
8 |
15 |
|
27 |
305 |
|
2 |
12 |
13 |
|
5 |
6 |
16 |
|
27 |
317 |
|
2 |
11 |
14 |
|
4 |
7 |
16 |
|
27 |
321 |
|
2 |
10 |
15 |
|
3 |
8 |
16 |
|
27 |
329 |
|
1 |
12 |
14 |
|
2 |
9 |
16 |
|
27 |
341 |
|
1 |
12 |
14 |
|
4 |
6 |
17 |
|
27 |
341 |
|
2 |
9 |
16 |
|
4 |
6 |
17 |
|
27 |
341 |
|
1 |
11 |
15 |
|
3 |
7 |
17 |
|
27 |
347 |
|
1 |
10 |
16 |
|
2 |
8 |
17 |
|
27 |
357 |
|
3 |
6 |
9 |
10 |
4 |
5 |
8 |
11 |
28 |
226 |
|
2 |
6 |
9 |
11 |
3 |
5 |
8 |
12 |
28 |
242 |
|
1 |
8 |
9 |
10 |
4 |
5 |
6 |
13 |
28 |
246 |
|
2 |
5 |
10 |
11 |
3 |
4 |
9 |
12 |
28 |
250 |
|
1 |
6 |
10 |
11 |
3 |
4 |
8 |
13 |
28 |
258 |
|
1 |
6 |
9 |
12 |
2 |
5 |
8 |
13 |
28 |
262 |
|
1 |
5 |
10 |
12 |
2 |
4 |
9 |
13 |
28 |
270 |
|
1 |
5 |
10 |
12 |
3 |
4 |
7 |
14 |
28 |
270 |
|
1 |
6 |
8 |
13 |
3 |
4 |
7 |
14 |
28 |
270 |
|
1 |
4 |
11 |
12 |
2 |
3 |
10 |
13 |
28 |
282 |
|
1 |
6 |
7 |
14 |
2 |
3 |
10 |
13 |
28 |
282 |
|
1 |
5 |
8 |
14 |
3 |
4 |
6 |
15 |
28 |
286 |
|
3 |
12 |
13 |
|
4 |
9 |
15 |
|
28 |
322 |
|
2 |
11 |
15 |
|
5 |
6 |
17 |
|
28 |
350 |
|
1 |
9 |
18 |
|
3 |
6 |
19 |
|
28 |
406 |
|
1 |
5 |
9 |
14 |
2 |
3 |
11 |
13 |
29 |
303 |
|
4 |
10 |
15 |
|
6 |
7 |
16 |
|
29 |
341 |
|
2 |
13 |
14 |
|
4 |
8 |
17 |
|
29 |
369 |
|
4 |
7 |
9 |
10 |
5 |
6 |
8 |
11 |
30 |
246 |
|
3 |
8 |
9 |
10 |
5 |
6 |
7 |
12 |
30 |
254 |
|
3 |
7 |
9 |
11 |
4 |
6 |
8 |
12 |
30 |
260 |
|
3 |
6 |
10 |
11 |
4 |
5 |
9 |
12 |
30 |
266 |
|
2 |
8 |
9 |
11 |
4 |
6 |
7 |
13 |
30 |
270 |
|
2 |
7 |
10 |
11 |
4 |
5 |
8 |
13 |
30 |
274 |
|
2 |
7 |
9 |
12 |
3 |
6 |
8 |
13 |
30 |
278 |
|
2 |
6 |
10 |
12 |
3 |
5 |
9 |
13 |
30 |
284 |
|
1 |
8 |
10 |
11 |
4 |
5 |
7 |
14 |
30 |
286 |
|
1 |
8 |
9 |
12 |
3 |
6 |
7 |
14 |
30 |
290 |
|
2 |
6 |
9 |
13 |
3 |
4 |
11 |
12 |
30 |
290 |
|
1 |
7 |
10 |
12 |
3 |
5 |
8 |
14 |
30 |
294 |
|
2 |
5 |
11 |
12 |
3 |
4 |
10 |
13 |
30 |
294 |
|
1 |
7 |
9 |
13 |
2 |
6 |
8 |
14 |
30 |
300 |
|
1 |
6 |
11 |
12 |
3 |
4 |
9 |
14 |
30 |
302 |
|
1 |
6 |
10 |
13 |
2 |
5 |
9 |
14 |
30 |
306 |
|
1 |
7 |
8 |
14 |
2 |
4 |
11 |
13 |
30 |
310 |
|
3 |
4 |
8 |
15 |
1 |
6 |
9 |
14 |
30 |
314 |
|
7 |
11 |
12 |
|
8 |
9 |
13 |
|
30 |
314 |
|
1 |
5 |
11 |
13 |
2 |
4 |
10 |
14 |
30 |
316 |
|
1 |
6 |
8 |
15 |
2 |
3 |
12 |
13 |
30 |
326 |
|
2 |
4 |
9 |
15 |
3 |
5 |
6 |
16 |
30 |
326 |
|
6 |
11 |
13 |
|
7 |
9 |
14 |
|
30 |
326 |
|
1 |
4 |
12 |
13 |
2 |
3 |
11 |
14 |
30 |
330 |
|
1 |
4 |
11 |
14 |
2 |
5 |
7 |
16 |
30 |
334 |
|
5 |
12 |
13 |
|
7 |
8 |
15 |
|
30 |
338 |
|
5 |
11 |
14 |
|
6 |
9 |
15 |
|
30 |
342 |
|
1 |
4 |
9 |
16 |
2 |
5 |
6 |
17 |
30 |
354 |
|
4 |
12 |
14 |
|
6 |
8 |
16 |
|
30 |
356 |
|
4 |
11 |
15 |
|
5 |
9 |
16 |
|
30 |
362 |
|
1 |
2 |
12 |
15 |
3 |
4 |
5 |
18 |
30 |
374 |
|
3 |
13 |
14 |
|
6 |
7 |
17 |
|
30 |
374 |
|
3 |
12 |
15 |
|
5 |
8 |
17 |
|
30 |
378 |
|
1 |
3 |
9 |
17 |
2 |
4 |
6 |
18 |
30 |
380 |
|
3 |
11 |
16 |
|
4 |
9 |
17 |
|
30 |
386 |
|
2 |
13 |
15 |
|
3 |
10 |
17 |
|
30 |
398 |
|
2 |
13 |
15 |
|
5 |
7 |
18 |
|
30 |
398 |
|
3 |
10 |
17 |
|
5 |
7 |
18 |
|
30 |
398 |
|
2 |
12 |
16 |
|
4 |
8 |
18 |
|
30 |
404 |
|
2 |
11 |
17 |
|
3 |
9 |
18 |
|
30 |
414 |
|
1 |
14 |
15 |
|
5 |
6 |
19 |
|
30 |
422 |
|
1 |
13 |
16 |
|
4 |
7 |
19 |
|
30 |
426 |
|
1 |
12 |
17 |
|
3 |
8 |
19 |
|
30 |
434 |
|
1 |
11 |
18 |
|
2 |
9 |
19 |
|
30 |
446 |
Table des égalités pour les entiers,
les carrés et les cubes jusqu'à une somme d'entiers égale à 40
|
a |
b |
c |
d |
aa |
bb |
cc |
dd |
S1 |
S2 |
S3 |
|
0 |
4 |
7 |
11 |
1 |
2 |
9 |
10 |
22 |
186 |
1738 |
|
1 |
5 |
8 |
12 |
2 |
3 |
10 |
11 |
26 |
234 |
2366 |
|
0 |
6 |
7 |
13 |
1 |
3 |
10 |
12 |
26 |
254 |
2756 |
|
2 |
6 |
9 |
13 |
3 |
4 |
11 |
12 |
30 |
290 |
3150 |
|
1 |
7 |
8 |
14 |
2 |
4 |
11 |
13 |
30 |
310 |
3600 |
|
0 |
5 |
10 |
15 |
1 |
3 |
12 |
14 |
30 |
350 |
4500 |
|
0 |
7 |
9 |
16 |
1 |
4 |
12 |
15 |
32 |
386 |
5168 |
|
3 |
7 |
10 |
14 |
4 |
5 |
12 |
13 |
34 |
354 |
4114 |
|
2 |
8 |
9 |
15 |
3 |
5 |
12 |
14 |
34 |
374 |
4624 |
|
1 |
6 |
11 |
16 |
2 |
4 |
13 |
15 |
34 |
414 |
5644 |
|
0 |
8 |
9 |
17 |
2 |
3 |
14 |
15 |
34 |
434 |
6154 |
|
1 |
8 |
10 |
17 |
2 |
5 |
13 |
16 |
36 |
454 |
6426 |
|
0 |
7 |
11 |
18 |
2 |
3 |
15 |
16 |
36 |
494 |
7506 |
|
4 |
8 |
11 |
15 |
5 |
6 |
13 |
14 |
38 |
426 |
5282 |
|
3 |
9 |
10 |
16 |
4 |
6 |
13 |
15 |
38 |
446 |
5852 |
|
2 |
7 |
12 |
17 |
3 |
5 |
14 |
16 |
38 |
486 |
6992 |
|
1 |
9 |
10 |
18 |
3 |
4 |
15 |
16 |
38 |
506 |
7562 |
|
0 |
8 |
11 |
19 |
1 |
5 |
14 |
18 |
38 |
546 |
8702 |
|
0 |
6 |
13 |
19 |
1 |
4 |
15 |
18 |
38 |
566 |
9272 |
|
2 |
9 |
11 |
18 |
3 |
6 |
14 |
17 |
40 |
530 |
7900 |
|
1 |
8 |
12 |
19 |
3 |
4 |
16 |
17 |
40 |
570 |
9100 |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/MulPuiIn.htm |
![]()