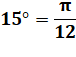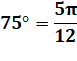|
Édition du: 04/02/2024 |
|
INDEX |
RECTANGLE |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Rectangle d'Ailles
Rectangle
très utile pour calculer les sinus et cosinus des angles 15° et 75° en
traçant un triangle inscrit dans le rectangle. Ce sont notamment des angles en Pi/12. |
||
|
|
Sommaire de cette page >>> Rectangle d'Ailles >>> Rectangle d'Ailles avec triangles >>> Table des lignes trigonométriques >>> Propriétés >>> Triangles spéciaux >>> D'autres triangles spéciaux ? |
Débutants Glossaire |
|
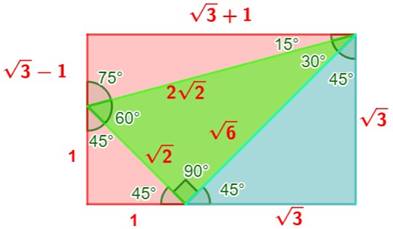
Le rectangle Rectangle
dont les dimensions sont en racine de 3. Très
utile pour calculer les sinus et cosinus des angles 15° et 75° en traçant un
triangle inscrit dans le rectangle. Rappel
Douglas S. Ailles Professeur au Kipling Collegiate Institute de
Toronto. Auteur de livres de maths pour les écoles. |
|
|
|
Deux présentations Un
triangle a pour sommets
-
soit du sommet
du même, -
sommet opposé, soit d'un autre
sommet. Dans les
deux cas, il y a au moins un triangle isocèle rectangle (deux angles à 45°).
Il est situé:
Dans les
deux cas, on trouve un triangle rectangle (30°, 60°), le célèbre triangle
rectangle des équerres d'écolier et dont les proportions sont: Dans les
deux cas, on trouve aussi un triangle rectangle (15°, 75°). |
|
|
|
Les valeurs de
cette table se déduisent immédiatement en observant le triangle dans le
rectangle d'Ailles. |
|
|
Voir Calculs
par l'algèbre / Brève
57-1132
|
Angles |
Tous les angles sont des nombres entiers de
degrés (rationnel en radians). Par opposition, les triangles de Pythagore n'ont
jamais d'angles aigus rationnels. Leurs mesures sont transcendantales (Jack
S. Calcul – Fact2). |
|
|
Côtés |
De longueur exprimée avec au plus une racine.
Donc, longueur rationnelle ou quadratique. |
|
|
Définition On appelle ici, triangles spéciaux, des triangles
qui ont :
Quantité Il en
existe 14 dont 3 sont rectangles. Ils sont répertoriés dans les tables ci-contre.
Construction Ils sont tous construits à partir du rectangle
d'Ailles et du triangle
d'or. Par exemple deux triangles de type 1 (15-75-90)
réunis par le grand côté de l'angle droit donne le triangle spécial
(30-75-75) noté 11. Leur construction:
|
Triangles spéciaux élémentaires
Triangles spéciaux élémentaires et
composés
|
|
Voir Autres triangles particuliers
/ Triangles
héroniens (triangles en nombre entiers) / Construction
du triangle 36-72-72
|
Deux autres cas pour les triangles spéciaux ? Ces deux triangles ont été proposés par un
internaute répondant à une question de Mathematics: En fait, on y retrouve les triangles élémentaires
similaires (15-75-90, 45-45-90 et 30-60-90). |
|
|
Bonus
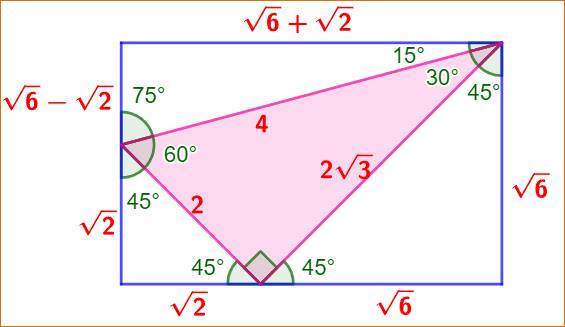
Ce triangle est similaire à l'un des triangles d'Ailles dans un rapport racine de 2.
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |