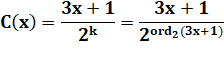Cycle de Collatz, les variantes

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/11/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suite de nombres
Débutants Général	Itérations – Cycles				Glossaire Suites et Séries
INDEX Rubriques	Suite de Fibonacci	Triangle de Pascal		Triangle de Leibniz
	Procédé de Kaprekar	Cycle de Syracuse		Cycle des Carrés
	Nombres Chanceux	Cycle de Syracuse Géné.
	Syracuse – Débutant		Sommaire de cette page >>> Les deux plus classiques >>> Les suites à l'envers >>> Arbre d Collatz >>> Extension aux nombres négatifs >>> La suite en 2n et 5n + 1 >>> Les suites voisines
	Syracuse – Développement
	Syracuse - Variantes
	Syracuse – Algèbre (2^x3^y)
	Syracuse – Tables
	Syracuse et nombre 27
	Syracuse – Programmation

Le PROBLÈME 3x + 1

Conjecture de Collatz

VARIANTES

Les recherches autour de cette simple conjecture sont passionnées. Il y a eu recrudescence des investigations depuis l'avènement des ordinateurs: aussi bien pour le profane qui cherche à se faire plaisir par ses découvertes que par les plus brillants mathématiciens qui cherchent toujours à démontrer la conjecture. Alors, d'autres suites ont émergé, sans égaler l'originale.

Voir Découverte Junior des cycles tels que celui de Syracuse / Conjectures

Les deux plus classiques (descente vers 1)
Suite normale	Suite compressée

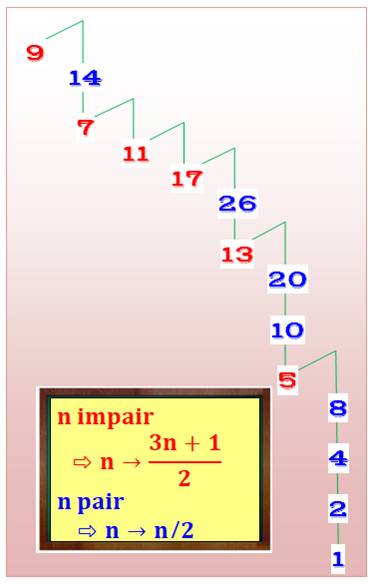
Dans les deux cas, un nombre pair est divisé par 2 autant que possible pour atteindre un nombre impair. On constate que, de toute manière, un nombre impair se transforme en nombre pair. Avec la forme compressée, la division par 2 est opérée systématiquement, supprimant une étape de calcul.
Dans tous les cas le nombre impair suivant est atteint avec la formule indiquée. Généralement, on ne s'intéresse qu'à la suite des nombres impairs qui est la même quelle que soit le type de suite envisagée.	Formule avec k = ord₂(3x+1): le plus grand entier tel que le dénominateur divise le numérateur. Exemple c(17) = 13, C(13) = 5 et C(5) = 1

Les suites à l'envers (montée à partir du 1)
Suite normale inverse	Suite compressée inverse

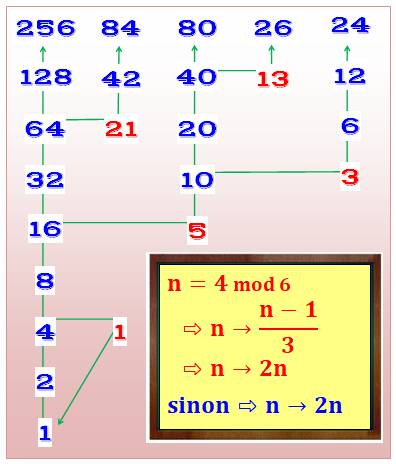
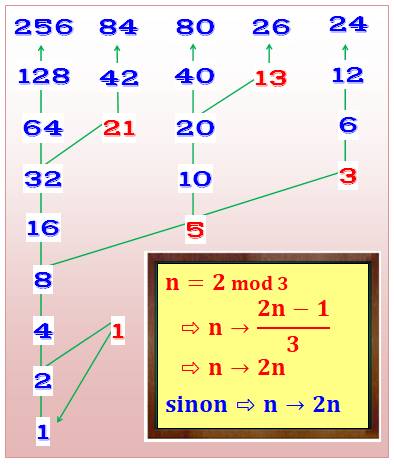
La suite est explorée à partir de 1. L'arbre se dédouble pour n ayant un reste de 4 lorsque divisé par 6 ( 4 mod 6) pour la suite inverse normale. La démonstration de la conjecture consiste, alors à prouver que tous les netiers sont atteint par les branches de l'arbre. Notez la formation de la boucle en bas de l'arbre.

Arbre de Collatz à 10 étages (suite compressée inverse)

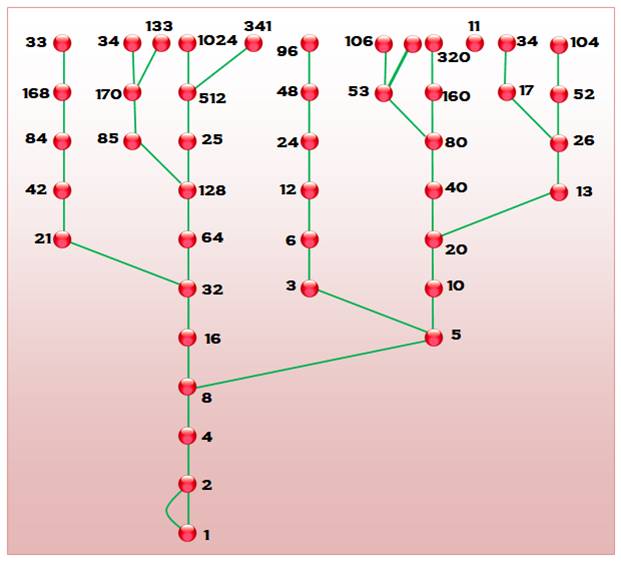
Voir Animation pour 19 étages en cercle – Jason Davies

Extension aux nombres négatifs
La transformation normale de Collatz des nombres négatifs engendrent de nombreuses boucles.	Nous sommes toujours avec n/2 et 3n + 1
Exemples (n, longueur, [suite]) -1, 1[-1, -2 …] -2, 1, [-2, -1…] -3, 5, [-3, -8, -4, -2, -1, -2…] -4, 3, [-4, -2, -1, -2 …] -5, 5, [-5, -14, -7, -20, -10, -5 …] -6, 6, [-6, -3, -8, -4, -2, -1, -2 …] -7, 5, [-7, -20, -10, -5, -14, -7 …] -8, 4, [-8, -4, -2, -1, -2 …] -9, 12, [-9, -26, -13, -38, -19, -56, -28, -14, -7, -20, -10, -5, -14 …] -10, 5, [-10, -5, -14, -7, -20, -10 …] … -17, 18, [-17, -50, -25, -74, -37, -110, -55, -164, -82, -41, -122, -61, -182, -91, -272, -136, -68, -34, -17 …] … -21, 24, [-21, -62, -31, -92, -46, -23, -68, -34, -17, -50, -25, -74, -37, -110, -55, -164, -82, -41, -122, -61, -182, -91, -272, -136, -68 …]	Exemple avec -13

La suite en 2n et 5n + 1
La suite est définie de la même manière que celle de Collatz en changeant le coefficient 3 par 5.	Exemples (n, longueur, [suite]) 1,5, [1, 3, 8, 4, 2, 1] 2, 2, [2, 1] 3, 6, [3, 16, 8, 4, 2, 1] 4, 3, [4, 2, 1] 5, 9, [5, 26, 13, 66, 33, 166, 83, 416, 208, 104, 52, 26, 13 …] 6, 7, [6, 3, 16, 8, 4, 2, 1] 7, ?, [7, 36, 18, 9, 46, 23, 116, 58, 29, 146, 73, 366, 183, 916, 458, 229, 1146, 573, 2866, 1433, 7166, 3583, 17916, 8958, 4479, 22396, 11198, 5599, 27996, 13998, 6999 …] 8, 4, [8, 4, 2, 1] 9, ?, [9, 46, 23, 116, 58, 29, 146, 73, 366, 183, 916, 458, 229, 1146, 573, 2866, 1433, 7166, 3583, 17916, 8958, 4479, 22396, 11198, 5599, 27996, 13998, 6999, 34996, 17498, 8749 …] 10, 31, [10, 5, 26, 13, 66, 33, 166, 83, 416, 208, 104, 52, 26, 13, 66, 33, 166, 83, 416, 208, 104, 52, 26 …]
Nous avons trois types de suite: suite se terminant par 1, comme pour toutes celles de Collatz (conjecture); suite aboutissant à une boucle (cas de n = 5 o u 10); ou suite qui semble se poursuivre jusqu'à l'infini (cas de n = 7 ou 9). Sans doute une suite divergente, mais à ce jour, ce n'est pas démontré. Nous ne savons pas non plus expliquer cette différence de comportement entre la 3n +1 et la 5n + 1.

Les suites voisines
En 3n – 1	En an + b
La suite se termine par 1 ou forme une boucle: Exemples (n, longueur, [suite]) 1, 1, [1] 2, 2, [2, 1] 3, 5, [3, 8, 4, 2, 1] 4, 3, [4, 2, 1] 5, 5, [5, 14, 7, 20, 10, 5, …] 6, 6, [6, 3, 8, 4, 2, 1] 7, 5, [7, 20, 10, 5, 14, 7, …] 8, 4, [8, 4, 2, 1] 9, 12, [9, 26, 13, 38, 19, 56, 28, 14, 7, 20, 10, 5, 14, …] 10, 5, [10, 5, 14, 7, 20, 10, …]	La suite se termine par 1 ou forme une boucle: Exemples avec n + 5 1, 1, [1] 2, 2, [2, 1] 3, 5, [3, 8, 4, 2, 1] 4, 3, [4, 2, 1] 5, 3, [5, 10, 5, …] 6, 6, [6, 3, 8, 4, 2, 1] 7, 8, [7, 12, 6, 3, 8, 4, 2, 1] 8, 4, [8, 4, 2, 1] 9, 10, [9, 14, 7, 12, 6, 3, 8, 4, 2, 1] 10, 2, [10, 5, 10, …]
Ces suites, comportant des boucles, présentent beaucoup moins d'intérêt que la suite de Collatz; ce qui illustre son originalité!

Autres …

D'autres suites on été imaginées:

Extension aux nombres rationnels,

avec nombres binaires,

avec nombre 2-adiques,

avec nombres complexes et débouché sur des fractales.

Retour	Syracuse – Développements
Suite	Syracuse – Algèbre (sommes en 2^x3^y) Syracuse – Tables Syracuse – Découverte junior Fractales et cycles Syracuse généralisée avec premiers et composés Autres, voir en haut de page
Voir	Boucle infernale Boucle SP (Somme x Produit) Calcul mental – Index Géométrie – Index Nombre Harshad Nombres narcissiques Nombres retournés Palindrome retard Preuve par neuf en pratique Récurrence Retournés et premiers Théorie des nombres – Index
Diconombre	Nombre 1 Nombre 2 Nombre 3
Sites	Voir Liste en page d'introduction
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Syracus4.htm