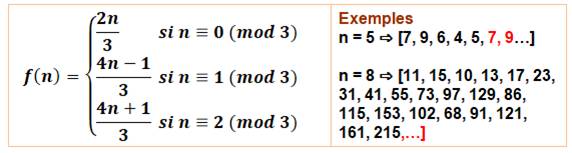|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Le CYCLE ou le PROBLÈME 3x + 1 Conjecture ou problème ou cycle ou transformation
Il s'agit d'une séquence très
simple d'opérations sur les nombres qui ramène toujours au même endroit, le
nombre 1. D'abord un amusement, cette étonnante suite
est devenue troublante pour les mathématiciens qui ne se lassent pas de
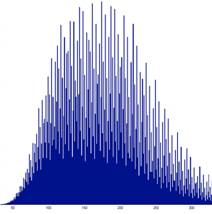
l'explorer sans avoir encore réussi à la domestiquer. Statistique sur les temps d'arrêt jusqu'à 100
millions => |
Voir Découverte Junior des cycles
tels que celui de Syracuse / Conjectures
En bref
|
|
Citations
|
Selon Paul Erdös
(1913-1996), Richard Guy (1983) et Jeffrey Lagarias (2010), les mathématiques
ne seraient pas encore assez mûres pour espérer résoudre cet innocent petit
problème.
1 Ripe (mûr) semble être l'original plutôt que
ready (prêt). Traduction: Les mathématiques sont sans doute pas prêtes (mûres) pour
de tels problèmes. Ne tentez pas de résoudre de tels problèmes. C'est un
problème extraordinairement difficile, complètement hors d'atteinte des
mathématiques actuelles. |
|
Le mathématicien Terence Tao vient
de démontrer que: Théorème La conjecture est "presque" vraie pour
"presque" tous les entiers. Presque vrai pour une
propriété P en math signifie que le rapport n(P) / n tend vers 1 pour n
tendant vers l'infini. Sachant que l'on compte n(P), la quantité de nombres
plus petits que n et vérifiant la propriété P. La démonstration de Terence Tao est plus générale
et s'applique à une fonction f(n) qui associe un nombre réel à un entier n et
qui tend vers l'infini lorsque n tend vers l'infini. Il choisit des entiers
représentatifs. Pour cette conjecture, il s'agit de la congruence par toutes
les puissances de 3. Cette démonstration ne conclut pas que
l'aboutissement est le nombre 1, mais passe toujours par un minimum. Tao
conclut: You can get as close as you want to the Collatz conjecture, but it’s
still out of reach. (La conjecture de Collatz peut être approchée d'aussi
près que l'on veut, mais elle est toujours hors de portée). Tous les nombres jusqu'à environ 1020
ont été testés positivement à cette conjecture. |
|
|
|||
|
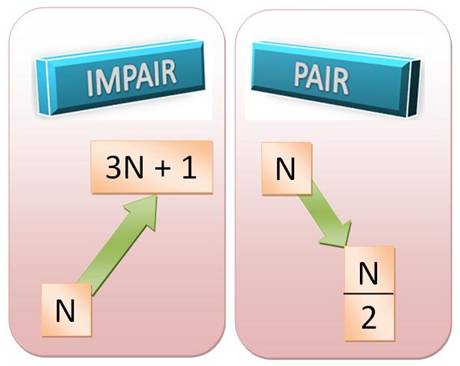
Approche
si le
nombre est impair on le gonfle s'il est
pair on l'amorti.
Règle
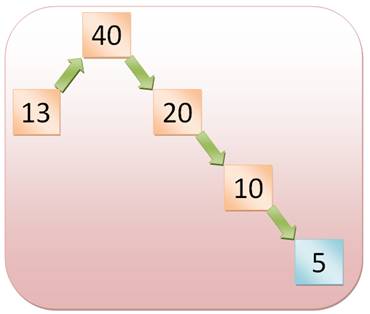
Exemple départ avec 5
La procédure nous entraîne vers 1. En poursuivant nous entrons dans une boucle avec le 4. Exemple départ avec 13
Après quelques étapes, nous rencontrons le 5, objet de
l'exemple précédent. Avec 13, la procédure conduit également vers le 1 et sa
boucle en 4. |
|||
|
|
||
|
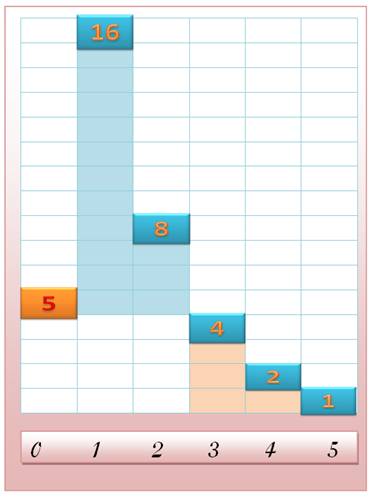
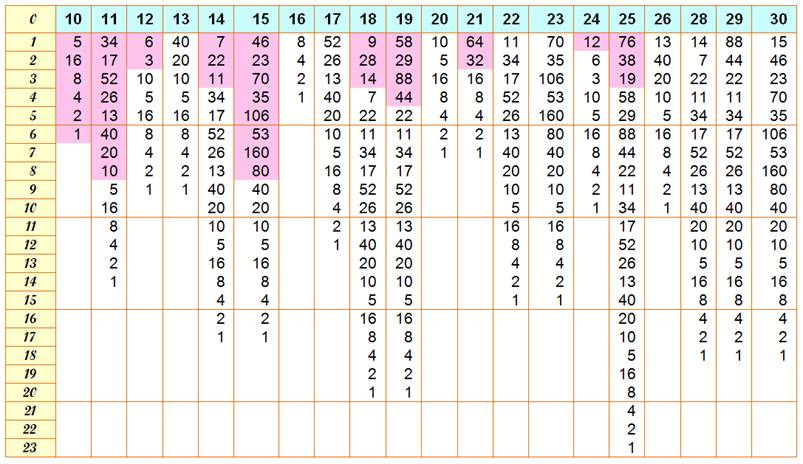
Quantité
d'étapes pour atteindre le nouveau passage par n (en rose).
Numérateur
= max / 2, et Note: chaque auteur précise ces notions en tête
de leurs articles. |
Voir
ce même graphique pour
n = 27 |
|
|
|
|
|
Conjecture Pour tout n, la fin de cycle est 1. Pas encore
démontrée, mais vérifiée jusqu'à n = 1020 .
Voir Présentation
sous forme d'un arbre On donne le nombre et son temps de
vol (comme 7 avec un temps de vol de 16). Le nombre qui suit est celui qui
produit un temps de vol supérieur (ici 9 avec un temps de vol de 19). On a effectivement: [7,
22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] – 16 étapes [8,
4, 2, 1] [9,
28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] Voir Programme Table des records de
durée de vol pour n de 1 à 1 000 000
J'ai
été étonné de trouver (chez beaucoup d'amateurs de cette suite) un nombre
pair le 54 (vol 112) juste après le 27 (vol 111), ce qui me semble une
évidence car 54 est l'antécédent de 27 (54/2) et dans ce cas 108, 216, etc.
vont être des records trop faciles à atteindre. En
fait seul les multiples de 3 sont des records intéressants car ils n'ont pas
d'antécédents en dehors des multiples de 2, les nombres de la forme 3x+1 ou
3x+2 ont un antécédent relativement simple à calculer. Puisqu'on parle de
vol, disons qu'ils sont sur la même "ligne". Par
exemple j'ai trouvé ce record sur le site Calculis:
durée de vol 2284 du nombre 2361235441021745907775 avec la Calculatrice en ligne webCalc. N =
2361235441021745907775 (3x + 1) pour remonter vers l'antécédent on calcule
[(N – 1)/ 3] × 4 + 1 car les
successeurs des nombres de la forme 4X + 1 sont 3 × (4X + 1) + 1 = 4 × (3X + 1) soit 3X + 1
après les divisions par 2. 3148313921362327877033 (3x + 2) dans
ce cas il faut multiplier par 2 ce qui nous ramène à un nombre de la forme 3 × (2x + 1) + 1 et on peut calculer [(N – 1) / 3] × 4 + 1 8395503790299541005421 (3x + 1) 11194005053732721340561 (3x + 1) 14925340071643628454081 (3x + 0) =3 × 4975113357214542818027 fin de la remontée mais nouveau
RECORD. Calcul des antécédents: 7 (3 × 2 +
1) antécédent 9= 4 × 2 + 1
=> 3 × 9 + 1 = 28 => 14 => 7 25 (3 × 8 +
1) antécédent 33= 4 × 8 +
1 73 (3 × 24 + 1) antécédent 97= 4 × 24 + 1 97 (3 × 32 + 1) antécédent 129= 4 × 32 + 1 |
|
Voir Cas du nombre
27/ Suite en Tables valeurs et records
Organisation
en rond des suites de Collatz
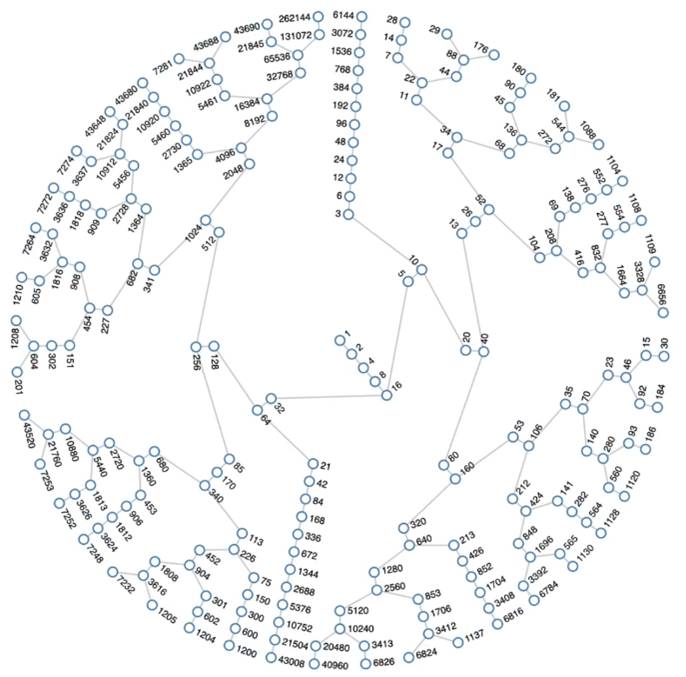
Extrait de
la séquence animée sur 19 itérations de Jason Davies – À voir
absolument!
Figure aussi
en Mathematician
Proves Huge Result on ‘Dangerous’ Problem – Kevin Hartnett
Représentation
esthétique en arbre (il en existe d'autres de ce type)

|
|
|
|
Il existe une constante C telle que, si n est
assez grand, alors le nombre de valeurs inférieures à n qui atterrissent en 1
est supérieur à nC.
Cycle
Approche
probabiliste
Voir Point
de la situation concernant la démonstration |
|
|
|
|
|
Photo de
1990 => Dans les
années 1930, il étudie les œuvres d'Edmund Landau, Oskar Petron et Isaac
Schur. Il s'intéresse aux fonctions en théorie des nombres et à la théorie
des graphes. Il a l'idée de conjuguer les deux domaines et de s'interroger
sur la structure graphes en relations avec le comportement des fonctions. En 1932,
il s'intéresse à une fonction qui progresse selon le mod 3 (voir encadré).
Il
formalise la conjecture qui porte son nom en 1937 sans la publier. En 1950,
il la présente dans divers séminaires. En 1952, il la présente à Helmut
Hasse, lequel la diffuse à l'université de Syracuse. De son côté, Stanislas
Ulam en fait état au Laboratoire national de Los Alamos. La conjecture
atteint Yale et Chicago dans les années 1960 avec Shizuo Kakutani. Elle créa
un tel engouement auprès des mathématiciens durant la guerre froide que
certains plaisantaient en faisant croire à un complot soviétique destiné à
ralentir le recherche américaine.
De
nombreux mathématiciens se sont cassés les dents sur un problème pourtant
bien simple en apparence. La conjecture à ce jour n'est toujours pas
démontrée. Elle a été testée à maintes reprises avec de puissants moyens de
calcul. Le record actuel est de 262 (= 4.6… 1018)
obtenu par Tomas Oliveira e Silva depuis 2009.
|
|
|
|
|
|
|
|
Voir Variantes du
cycle de Collatz
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Article |
|
|
Diconombre |
|
|
Livres |
|
|
Animation Interactif |
|
|
Sites |
|
![]()