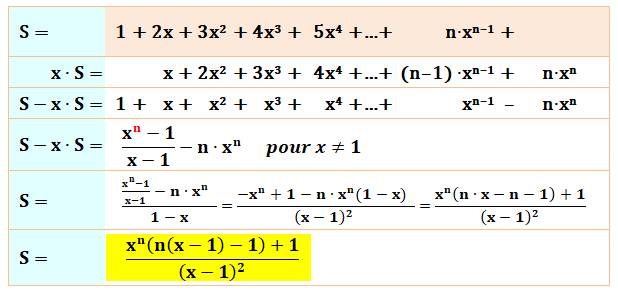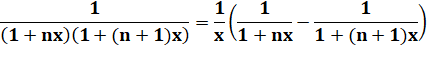NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/10/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	IDENTITÉS
Débutants Addition	SOMMES Nombres et puissances					Glossaire Addition
INDEX Identités Puissances	Index et Formules		Entiers	Carrés	Cubes
	Somme des puissances de 2 à 20 des nombres successifs
	Nombre somme de puissances
	Somme d'un nombre à des puissances successives
	Somme d'expression en x et puissances successives
		Sommaire de cette page >>> Somme en x et puissances successives >>> Somme pyramide en x >>> Somme en 1/f(x) et puissances successives >>> Inverse de produits en x >>> Inverse de produits en x – BIS >>> Somme pyramide en x

SOMMES d'expressions en X

& puissances successives

Algèbre avancé

Somme en x et puissances successives
Puissances de x pondérées par les nombres entiers successifs (x réel différent de 1)
Exemple avec quatre façons d'exprimer cette somme Graphe de la fonction
Démonstration En passant par la somme d'une suite géométrique de raison x
Cas x = 1	Avec x = 1, a division par (x – 1) n'est pas légitime, mais un simple calcul direct montre qu'il s'agit de la somme des entiers:
Cas de x = – 1	Avec x = –1, il s'agit de la somme alternée des entiers Ex: x = – 1 et n = 5 => S = (1+ (-10-1) (-1)^5 ) / (-2)^2 = 12 / 4 = 3 Et avec la formule pour – 1: S = (-1)^4 x plafond (5/2) = 1 x 3 = 3
Limite	Pour x < 1 S = 1 + 2x + 3x^2 + 4x^3 +… S – xS = 1 + x + x^2 + x^3 +… = 1 / (1 – x) Progression géométrique avec q = x < 1 S = 1 / (1 – x)^2 Avec x 1 (pour x= 1, somme triviale de 1). Exemple avec x = 1/2 S = 1 + 1 + 3/4 + 4/8 + … = 1 / (1/2)² = 4 Exemple avec x = –0,9 En bleu, la valeur limite, et en dessous, les valeurs pour k = 100. Quelques valeurs
Récurrence	Chaque terme se déduit des deux précédents par la formule de récurrence: Exemple: U4 = 2x . U3 – x² . U2 = 2x.3x² – x².2x = 6x^3 – 2x^3 = 4x^3

Voir Suite Harmonique

Somme en 1/f(x) et puissances successives
Somme fractionnaire avec x réel et puissances successives Voir Cas particuliers de x = 1 et x = –1
Exemple Avec les diverses façons d'exprimer la somme Notez qu'avec n = 5, il y a bien 6 termes (de 0 à 5)
Exemple avec x = 1,1 et k = 7
Valeurs La formule est valable pour tout x réel différent de 1 et –1. Pour x = 0, on retrouve la somme des puissances de 2: S = 1 + 2 + 4 + 8 = 15 = 16 – 1: (Voir points rouges sur le graphe). Pour x = 1, S = demi somme des puissances de 2. S = 1/2 + 2/2 + 4/2 + 8/2 = 15,5 Pour x = –1, la division par zéro est impardonnable. Le graphe montre bien cette valeur singulière de x (y tend vers l'infini).
Limite
Exemples	Pour x = 2, la série converge vers 1 Valeur proche de 1 avec seulement quatre termes. Pour x = 3, limite = 1/2 avec trois termes => S = 1/2 – 0,0012… avec quatre termes => S = 1/2 – 0,000000371… Convergence rapide. Avec des valeurs comprises entre – 1 et + 1, la série diverge. Exemple: avec x = 0,5 et n = 10 S = 2 046 = 2^11 – 2

Inverse de produits en x
Somme de la série:
Pour chaque terme Voir Identité	…
Addition des termes
Identité inversée
Exemple (x = 1)

Voir Nombre 0,25

Inverse de produits en x – BIS
Somme de la série:
Ènième terme
En somme de deux fractions
Égalité des numérateurs
Avec 1 + a^n-1x = 0
Avec 1 + a^nx = 0
Retour à Tn
Termes	…
Somme
Exemple avec x = 1 a = 2 n = 2

Somme pyramide en x
Pyramide en x	1 + 1+ x + 1+ x + x² + 1+ x + x² + x^3 1+ x + x² + x^3 + … + x^n-1
Exemple x = 2	1 + 1+ 2 + 1+ 2 + 4 + 1+ 2 + 4 + 8 1+ 2 + 4 + 8 + 16	62 = 57

Merci à Claude M. pour sa contribution

Retour	Somme d'un nombre à des puissances successives
Suite	Somme des puissances de 2 à 20 Formules avec les puissances 4 Toutes les formules de somme Nombres de Bernoulli et sommes de puissances
Table	Carrés, cubes … et leurs cumuls
Voir	Carrés Constantes Cubes Factorielles et somme des entiers Isopérimètre Nombres consécutifs Index Nombres de Bernoulli Nombres géométriques Pairs et impairs Somme des puissances des nombres successifs - Holopotentiel Tautochronie Théorèmes
Cette page	http://villemin.gerard.free.fr/aMaths/Sommes/SomPuisX.htm