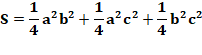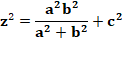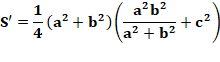|
Édition du: 14/01/2024 |
|
INDEX |
Théorème de Pythagore |
|||
![]()
|
Démonstrations du Théorème de Pythagore par calcul des aires Revue des
nombreuses démonstrations de ce célèbre théorème dit de Pythagore. |
||
|
|
Sommaire de cette page >>>
Démonstration du président Garfield >>>
Démonstration avec trapèze >>>
Démonstration avec parallélogrammes >>>
Démonstration avec hexagone >>>
Démonstration avec double triangles >>>
En trois dimensions (tétraèdre) |
Débutants Glossaire |
Voir Types de démonstrations
du théorème de Pythagore
|
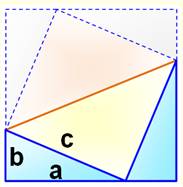
Cette démonstration considère la figure en forme de trapèze
constituée de deux triangles rectangles identiques bleus et du triangle
rectangle en jaune. Deux évaluations de l'aire du trapèze:
|
|
||||||||
|
En fait, c'est une variante de la méthode par
échange de triangles. Il suffit de tracer le complément (en pointillés) pour
s'en rendre compte. |
Coin historique
|
||||||||
|
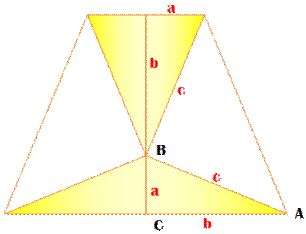
Le triangle de base ABC est répété quatre fois. La figure forme un
trapèze. Les deux triangles à gauche et à droite sont isocèle (côté c) et
rectangle (complémentarité des angles dans les triangles rectangles.
Note: on aurait pu ne travailler
que sur le trapèze rectangle à droite (ou à gauche) et retrouver le même
résultat. |
|
|||||||||
|
Construction On utilise la figure des trois carrés
construits autour du triangle rectangle. On duplique le grand carré vers le haut (petit pointillé). On s'intéresse au parallélogramme jaune KMAP puis à son voisin KMBQ en
montrant que les aires valent a² et b²
et qu'elles contribuent à former l'aire c².
Démonstration Avec ses côtés parallèles et son angle droit en M, le quadrilatère
MGKF est un rectangle de côté a et b et de diagonale c. Les deux angles
complémentaires en M sont égaux à ceux du triangle originel. Par conséquent,
KM est parallèle à AD et à BC. |
|
||
|
On a ainsi: KM parallèle à PA et de même longueur c. On a aussi: AM parallèle à EF ou PK. Le quadrilatère KMAP est un parallélogramme. Avec la base AM et la hauteur FM, son aire vaut b². Avec la base KM et la hauteur AR, son aire vaut c.AR. On montre de la même manière que KMBQ est un parallélogramme et son
aire s'exprime également de deux
façons. |
|
||
|
Construction Le triangle est tripliqué sur les côtés du carré ABCD. On trace la droite PQ (passant par M ?) Le principe consiste à évaluer l'aire du quadrilatère entouré de rose
de deux manières:
|
|
||
|
Démonstration Il s'agit de montrer que le point M, sommet du triangle AMB, est sur
PQ. On trace PM; le triangle APM est isocèle (AP = AM = b) et il est rectangle
(angle droit en A, par complémentarité); ses angles à la base valent 45% On trace QM; le triangle BQM est isocèle-rectangle et ses angles à la base valent 45°. La somme des trois angles en M (45 + 90 + 45 = 180°) montrent que les
points P, M et Q sont alignés.
|
Aires des triangles Triangle isocèle-rectangle APM: b²/2 Triangle isocèle-rectangle BQM: a²/2 Triangle rectangle AMB: ab/2 Aire de l'hexagone Aires des deux triangles: ab Aire du carré: c² Comparaison ab + c² = a² + b² + ab c² = a² + b² |
||
|
Construction Triangle rectangle ABD et son homologue tête-bêche AED. Droite BE. Le
triangle rectangle à considérer est ABC. Démonstration Avec les triangles semblables ABC et BCD: x = a² / b Avec les triangles semblables ACE et ECD: y = ac / b Aire ABC = 1/2 a. (b + x) = 1/2 a (b + a² / b) Aire AED = 1/2 c. y = 1/2 c (ac / b) Égalité: ab + a3 / b = ac² / b En multipliant par b et en divisant par a: b² +
a² = c² Intérêt
|
|
||
|
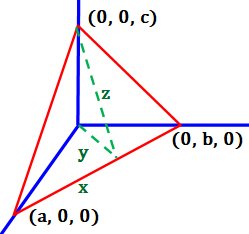
Soit un tétraèdre droit
avec ses côtés de longueurs (a, b et c). On s'intéresse aux triangles rectangles portés
par les côtés; la somme des carrés de leur aire: Et, maintenant, au triangle rouge qui est le
triangle "hypoténuse". Son aire est : x.z Le côté bas du triangle rouge: Relation dans le triangle
rectangle:
Le carré de l'aire du triangle hypoténuse: |
Le carré de l'aire du triangle
"hypoténuse" (rouge) est égal à la somme des carrés des aires
projetées (aires des triangles portés par les côtés – bleus). |
|
Voir Généralisation a n
dimensions
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/Aires.htm
|