NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Trois carrés	Quatre triangles	Heilbron	Carrés & triangles
	Médianes	Représentation	Brocard	Cercles et triangles
		Équilatéral 345		Démo fallacieuse
		Sommaire de cette page >>> Les trois carrés et les quatre triangles >>> Propriétés des deux carrés – Pythagore >>> Points de Vecten

TROIS CARRÉS sur le TRIANGLE

Figure de Vecten ou figure du Moulin à vent

Trois carrés dessinés sur les côtés d'un triangle quelconque engendrent trois triangles d'aires égales.

Étude de cette figure vers 1817par Vecten, professeur de mathématiques spéciales à Nîmes à cette époque.

Les trois carrés et les quatre triangles
Construction Un triangle DCG quelconque (pas forcément rectangle comme dans la démonstration du théorème de Pythagore). Les carrés construits sur les côtés. Les triangles verts construits à partir des sommets des carrés. Propriété Les triangles en vert ont la même aire que le triangle originel DCG. Bien noter Ils ne sont pas isométriques (superposables) mais ont la même aire.
Démonstration Les flèches montrent comment opérer une rotation de 90° des triangles bleus autour des sommets du triangle originel rose. Les nouveaux triangles isométriques aux premiers sont dans une position qui permet de comparer leur aire à celle du triangle originel. Ils ont la même longueur de base et la même hauteur: ils ont la même aire.

Propriétés avec deux carrés – Pythagore
Propriété Les deux triangles verts (ABD et ACM) sont isométriques. Démonstration ABD: base AD et hauteur AC; aire: b²/2 ACM: base AC et hauteur CE: aire: b²/2 Nous avons vu que le triangle EFC est égal au triangle ABC; c'est le cas aussi du triangle ECM dont l'angle en C vaut l'angle en A: Angle ECM = Angle BAC et, en ajoutant 90°, Angle DAB = angle ACM.
Égalité des triangles à gauche Les triangles ABD et ACM ont: un côté égal AD et AC = b un angle égal DAE = ACM la même aire (b²/2) Ils sont égaux (isométriques).	Orthogonalité DA orthogonal à AC Du fait de l'isométrie des triangles: AM est orthogonal à DB et MC est orthogonal à AB
Égalité des triangles à gauche Mêmes conclusions à droite avec le petit carré (segments en mauve): ABG = MCB d'aire a²/2. Autres propriétés remarquables Le demi-cercle qui inscrit le triangle rectangle ABC, inscrit également les triangles rectangles AIB (vert) et BJG (mauve). MC étant orthogonal à AB, sont prolongement CH est une des hauteurs du triangle ABC.
Triangle MCH et MCB MCH: base MC et hauteur AH; aire: c . AH/2 = b²/2 MCB: base MC et hauteur HB; aire: c . HB/2 = a²/2	Théorème de Pythagore Somme des aires: c (AH + HB) = a² + b² c² = a² + b²

Source image CNRS

POINTS de VECTEN
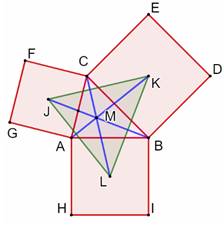
Contexte Vecten est un professeur de mathématique. En 1816, dans les Annales de Gergonne, il publie un article où figure cette propriété de la chaise de l'épousée construite sur un triangle quelconque : trois carrés adjacents aux côtés du triangle. Cette figure ressemble à celle servant à illustrer le fameux théorème de Pythagore s'appliquant aux triangles rectangles. Construction Triangle ABC et carrés extérieurs sur les côtés avec J, K et L pour centres. Le triangle JKL est le triangle de Vecten et son cercle circonscrit est le cercle de Vecten. Le point de concours des droites JB, KA et LC est le point de Vecten extérieur. C'est le point X(485) de la nomenclature de Kimberling Même construction avec les carrés internes et création du point de Vecten intérieur. C'est le point et X(486). Propriétés Les droites JB, KA et LC sont les hauteurs du triangle de Vecten. Le point M est son orthocentre. Les deux triangles (ABC et JKL) ont même centre de gravité. Les deux points de Vecten sont alignés avec: le point d'Euler X(5), et le point de Lemoine X(6). Relation AK² + BJ² + CL² = 3(AB² + BC² + CA²)		Carrés extérieurs Carrés intérieurs Relation – Notations
Coordonnées du point de Vecten extérieur Inverser les signes pour le point intérieur	Trilinéaires: Barycentriques:

Suite / Retour	Points Napoléon Quatre triangles Triangles et cercles	Triangles et triangles Théorème de Pythagore Théorème de Bottema
Voir	Allumettes Angle Arbres de distribution Carré dans le triangle, construction astucieuse Carrés Cercle DicoMot Droite Éléments de géométrie Géométrie – Index	Jeux et énigmes – Index Nombres triangles Polygone Relations dans les triangles Triangle – Index Triangle de Calabi et ses trois carrés dans le triangle Triangles Triangles – Types Trigonométrie
Sites	Trois carrés: la coiffe alsaciennes (page 19) – Patrice Debart – Voir cette page pour d'autres propriétés de cette construction ETC Kimberling X(485) Point de Vecten – Wikipédia La figure de Vecten – Étude – Jean-Louis AYME – pdf 143 pages Vecten Points – Wolfram MathWorld Dynamic Geometry Problem 1447: Outer Vecten Point - Animation
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/TroisCar.htm