NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ADDITION
Débutants Addition	PARTITION					Glossaire Addition
Index Partition	Entiers & Carrés		Cubes		Puissances 4...n
	Somme de 4 carrés Théorème de Lagrange			Somme de n puissances Théorème de Waring
	1 à 100 en 4 carrés
	Sommes de cubes et autres puissances			Comprendre les sommes de carrés
		Sommaire de cette page >>> Somme de 4 carrés >>> Somme de quatre carrés distincts >>> Carrés et somme de 2 carrés >>> Sommes 3 & 4 carrés >>> Couverture >>> Somme de carrés = nombres concaténés >>> Anglais

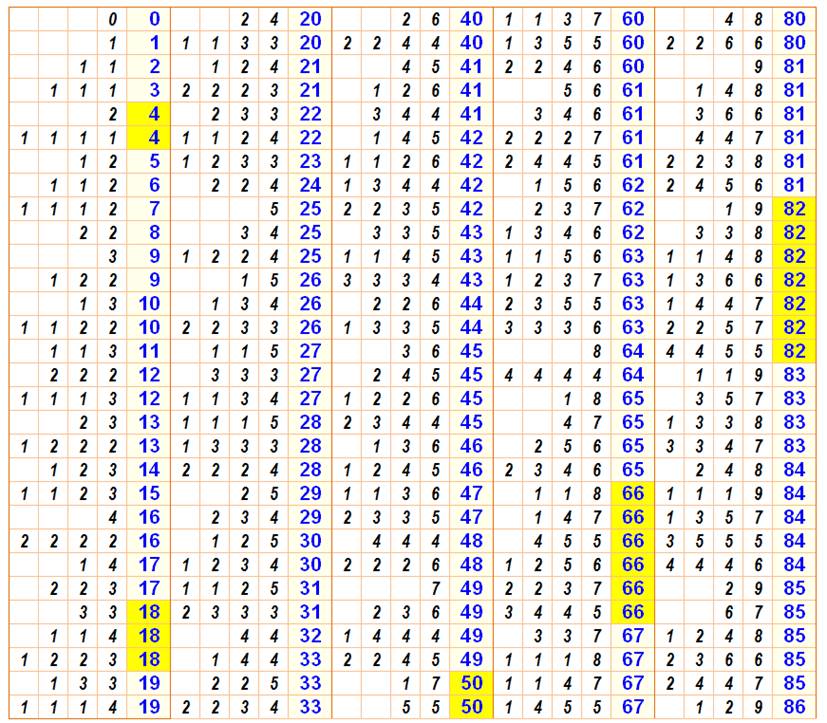
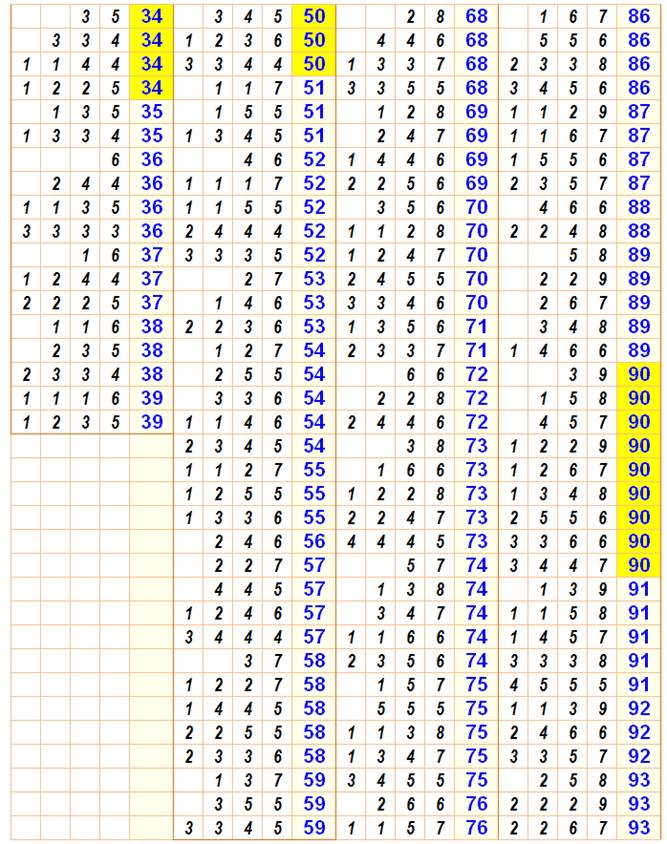
Théorème de Lagrange

Théorème de Bachet-Lagrange

Théorème de Fermat-Lagrange

Partition des nombres avec des carrés

Tout nombre entier est la somme de quatre carrés.

Propriété énoncée par Bachet de Méziriac, aussi par Fermat.

Souvent attribuée à Waring .

Démontrée par Lagrange en 1770.

Ensuite, Euler en a donné une démonstration élégante.

Jacobi a donné le nombre de manières dont cette décomposition est possible.

Legendre a montré qu'un nombres est somme de trois carrés, si et seulement s'il est de la forme 4^k . (8a – 7).

SOMME DE 4 CARRÉS
Théorème de Lagrange Tout entier est décomposable en somme d'au plus quatre carrés: N = A² + B² + C² + D² Suite Théorie sur la somme des carrés	Exemples 100 = 8² + 6² 101 = 9² + 4² + 2² 7 = 2² + 1² + 1² + 1² Les quatre carrés sont bien nécessaires pour le nombre entier 7. Historique Connu empiriquement de Diophante. Démontré en 1770 par Lagrange. Jacobi a trouvé la quantité de possibilités de décompositions.

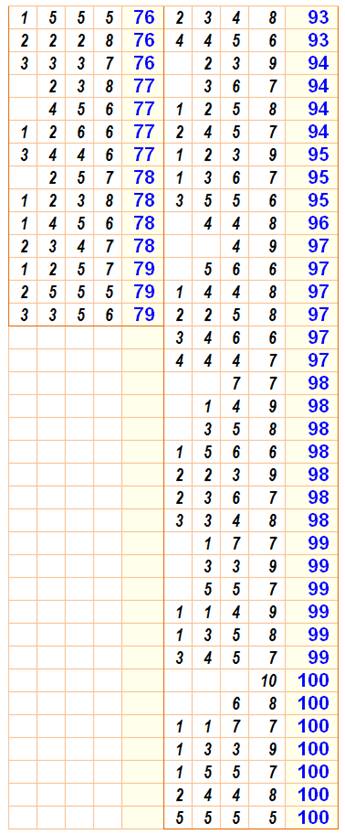
Somme de quatre carrés distincts

155 = 1² + 3² + 8² + 9² = 3² + 4² + 7² + 9² 157 = impossible 159 = 1² + 3² + 7² + 10² = 2² + 3² + 5² + 11² = 2² + 5² + 7² + 9² 161 = 3² + 4² + 6² + 10² 163 = 1² + 4² + 5² + 11² 165 = 1² + 2² + 4² + 12² = 2² + 4² + 8² + 9² = 2² + 5² + 6² + 10² = 4² + 6² + 7² + 8²

Tous les nombres impairs à partir de 159 sont somme de quatre carrés distincts non nuls. F. Halter-Kock

CARRÉS et somme de DEUX CARRÉS Tous les nombres de 0 à 100 couverts par une somme de 1 ou 2 carrés
0 = 0²	1 = 1²	2 = 1² + 1²	3	4 = 2²	5 = 2² + 1²	6	7	8 = 2² + 2²		9 = 3²
10 = 3² + 1	11	12	13 = 3² + 2²	14	15	16 = 4²	17 = 4² + 1	18 = 3² + 3²		19
20 = 4² + 2²	21	22	23	24	25 = 5²	26 = 5² + 1	27	28		29 = 5² + 2²
30	31	32 = 4² + 4²	33	34 = 5² + 3²	35	36 = 6²	37 = 6² + 1²	38		39
40 = 6² + 2²	41 = 5² + 4²	42	43	44	45 = 6² + 3²	46	47	48		49 = 7²
50 = 5² + 5² = 7² + 1	51	52 = 6² + 4²	53 = 7² + 2²	54	55	56	57	58 = 7² + 3²		59
60	61 = 6² + 5²	62	63	64 = 8²	65 = 8² + 1² = 7² + 4²	66	67	68 = 8² + 2²		69
70	71	72 = 6² + 6²	73 = 8² + 3²	74 = 7² + 5²	75	76	77	78		79
80 = 8² + 4²	81 = 9²	82 = 9² + 1²	83	84	85 = 9² + 2² = 7² + 6²	86	87	88		89 = 8² + 5²
90 = 9² + 3²	91	92	93	94	95	96	97 = 9² + 4²	98 = 7² + 7²		99
100 = 10² = 8² + 6²

Toutes les SOMMES de 1 à 4 CARRÉS Pour tous les nombres de 0 à 100 couverts (en jaune le record et quantité de présentations)
Exemple de lecture: 20 = 2² + 4² = 1² + 1² + 3² + 3² 90 est neuf fois somme de jusqu'à quatre carrés

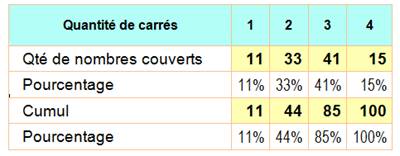
Voir Pourcentage

Voir Tables – Index

Somme de carrés = nombres concaténés

Somme = nombres concaténés

Tous les motifs jusqu'à 10 000 et un motif pour des nombres plus grands.

La recherche par ordinateur est assez longue.

10² + 1²	=	101
10² + 100²	=	10 100
12² + 33²	=	1 233
88² + 33²	=	8 833
588² + 2 353²	=	5 882 353
990² + 100²	=	990 100
9 412² + 2 353²	=	94 122 353

98939412² + 10243728²

=

9893941210243728

Suite Nombres carrés et concaténation

ENGLISH CORNER

Lagrange's Four Square Theorem was proved in 1770 by Joseph Louis Lagrange This statement was first stated in 1621 by Bachet, and is also known as Bachet's Conjecture. Also conjectured by Fermat in 1640. It states that every natural number is the sum of at most four squares. More formally, for every positive integer n there exist non-negative integers a, b, c, d such that n = a² + b² + c² + d². Adrien-Marie Legendre improved on the theorem in 1798 by stating that a positive integer can be expressed as the sum of at most three squares if and only if it is not of the form 4^k . (8a – 7). His proof was incomplete, leaving a gap which was later filled by Karl Friedrich Gauss.

Suite	Théorie sur la somme des carrés Somme de n puissances Théorème de Waring
Aussi	S'y retrouver Théorie sur la somme des carrés Table des nombres de 1à 100 Toutes les présentations de partitions des nombres jusqu'à 100 en somme de 2 carrés
Voir	Bi, tripartitions Carré des triangulaires = somme de cubes Cubes Nombre = sommes de cubes Nombre = sommes de puissances Nombres carrés Nombres cubes Nombres polygones Nombres triangles Somme multi puissantes Unité des puissances
Sites	OEIS A004215 - Numbers that are the sum of 4 but no fewer nonzero squares. Lagrange et la variation des théorèmes – CNRS – Pierre de la Harpe – 2014 Théorème des quatre carrés de Lagrange – Wikipédia Somme de carrés – Univesité de Lille Décomposition d'un entier en somme de carrés
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThLagran.htm