< NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/05/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres en forme
Débutants Général	Somme des chiffres				Glossaire Général
INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Types de nombres Jeux et énigmes Puissance Décomposition	Sommes des chiffres		Racine numérique	Cycle des carrés
	Sommes des Ch de n^k		Narcissique	k-narcissiques
	Digipuissants		Faute de frappe	Puissances consécutives
		Sommaire de cette page >>> Narcissiques généralisés >>> Somme des puissances des chiffres >>> Les k-narcissiques jusqu'à n = 100 000 >>> Les plus petits >>> Nombres expository de Keith

NOMBRES NARCISSIQUES (suite)
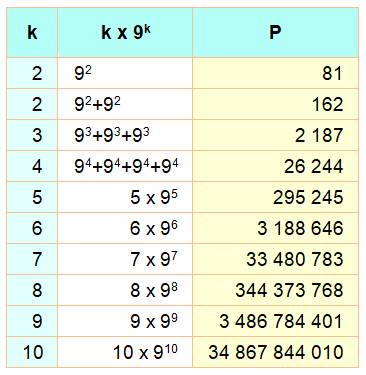
Nombres K-narcissiques Nombre égal à k fois la somme des puissances de ses chiffres. Exemple avec k = 2 et des cubes 702 = 2 (7^3 + 0^3 + 2^3) = 2 (343 + 8) = 2 x 351 Avec k = 1, le nombre est un pur narcissique.	Nombres narcissiques généralisés Nombre égal à une fonction linéaire de la somme des puissances de ses chiffres. Exemple 336 = 3+3+6 + 3^2+3^2+6^2 + 3^3+3^3+6^3 = 12 + 54 + 270
Nombres expository de Keith Nombre égal à une combinaison des sommes des chiffres du nombre, du carré, du cube, etc. et, dans chaque cas, mis à une puissance particulière. Les multiples sont autorisés Exemple avec k = 2 et des cubes Le nombre 336 est égal à la somme de ses chiffres à la puissance 1, 2 et 3. Le nombre 39 est égal à la somme de ses chiffres de ceux de son carré et sa puissance quatrième.

Voir Narcissiques et leurs cousins.

Narcissiques généralisés
Codage du type S = somme 1 = somme des chiffres 2 = sommes des carrés 3 = somme des cubes S233 = somme des carrés et deux fois somme des cubes Tableau Toutes les configurations en sommes de chiffres, carrés et cubes de 1 à 3 fois chacune. Remarquables 153 336 666 1998 Le nombre 1998 est le maximum atteignable de la sorte (cubes).
Tableau des nombres narcissiques généralisés jusqu'à la puissance 6 Avec répétition jusqu'à trois fois pour n jusqu'à 10 000 Le nombre 978 460 est le plus grand de la sorte (puissance 6). Somme maximale des chiffres à une puissance k Exemple de lecture: pour un nombre de quatre chiffres (Max = 9999), la somme des puissances quatrièmes est 26 244 qui est plus que Max. Inutile d'explorer plus loin avec des nombres de quatre chiffres.

Somme des puissances des chiffres
Table des nombres n = 10 à 50 et la sommes de leurs chiffres à la puissance p. En rouge, les sommes multiples ou sous-multiples du nombre n: les k-narcissiques. Comme 3 x 4 = 12 ou 72 = 3 x 24. Évolution

Les k-narcissiques jusqu'à n = 100 000
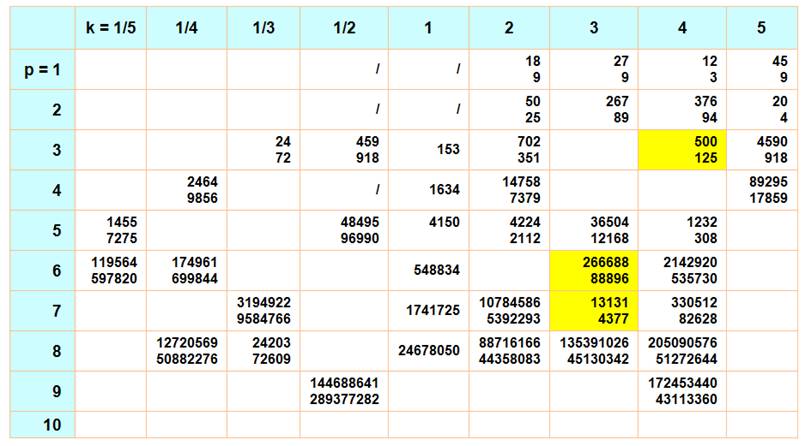
Cette table recense tous les k-narcissiques des nombres n de 10 à 100 000 Avec k variant de 1/5 à 5 Et les puissances de 1 à 5 des chiffres de n. En jaune, les nombres narcissiques (k = 1). Exemples de lecture n = 1 455 = 1/5 (1^5 + 4^5 + 5^5 + 5^5) = 7 275 / 5 = SC / 5 n = 24 203 = 1/3 (2^8 + 4^8 + 2^8 + 0^8 + 3^8) = 72 609 / 3 = SC / 3

Les plus petits k-narcissiques

Recensement du plus petit k-narcissique dans sa catégorie, selon le facteur multiplicatif k et la puissance p appliquée aux chiffres pour n jusqu'à 300 millions. Le tableau indique le plus petit dans sa catégorie. On donne le nombre N et la somme S de ses chiffres à la puissance p. En tête de colonne le rapport entier k entre N et S. Exemples de lecture n = 18 = 2 (1 + 8) = 2 x 9 n = 1455 = 1/5 (1^5 + 4^5 + 5^5 + 5^5) = 7 275 / 5 En jaune, chiffres remarquables. Le cas p = 1, nombre égal à k fois la somme de ses chiffres, fait l'objet d'une page spéciale (Nombres de Harshad).

Nombres narcissiques de Keith (expository)		haut
Nombres expository de Keith à deux termes T1 et T2 (sans doute les seuls). Pour 12, on note s1113 : 1 pour chiffres er 1 pour puissance 1; puis 1 pour chiffres et 3 pour leur cube. Pour 233, on note s2132: 2 pour les chiffres du carré et 1 pour la puissance 1; puis 3 pour les chiffres du cube et 2 pour leur carré. Autres exemples (avec plus de deux termes)
45 = 4+5 + 9+1+1+2+5 + 4+1+0+0+6+2+5 = 2+0+2+5 + 9+1+1+2+5 + 4+1+0+0+6+2+5 Voir DicoNombre 45	s11 31 41ou s21 31 41 45^2 = 2 025 45^3 = 91 125 45^4 = 4 100 625
48 = 4+8 + 2+3+0+4 + 5+3+0+8+4+1+6 Voir DicoNombre 48	s11 21 41 48^2 = 2 304 48^4 = 5 308 416
50 = 2+5 + 1²+2²+5² + 6+2+5 Voir DicoNombre 50	s21 22 41 50^2 = 2 500 50^4 = 6 250 000
51 = 5+1 + 1+3+2+6+5+1 + 3+4+5+0+2+5+2+5+1 Voir DicoNombre 51	s11 31 51 51^3 = 132 651 51^5 = 345 025 251
57 = 5+7 + 3+2+4+9 + 1+8+5+1+9+3 Voir DicoNombre 57	s11 21 31 57^2 = 3 248 57^3 = 185 193
57 = 5+7 + 1+8+5+1+9+3 + 1+5+5+6+1	s11 31 41 57^3 = 185 193 57^4 = 10 556 001
62 = 6+2 + 3+8+4+4 + 9+1+6+1+3+2+8+3+2 Voir DicoNombre 62	s11 21 51 62^2 = 3 844 62^5 = 916 132 832
336 = 3+3+6 + 3^2+3²+6^2 + 3^3+3^3+6^3 Voir DicoNombre 336	s11 12 13

Suite de cette Table en pdf

Voir Nombres et cycles de Keith / Brève 50-989

Suite	Somme des carrés des chiffres Somme des chiffres des puissances Somme-Produit des chiffres – Index
Voir	Automorphiques Facteurs sans zéro Nombres et puissances de leurs chiffres Palindromes Pannumériques Partition en puissance
Site	All Numbers Are Interesting: A Constructive Approach – Mike Keith - 1998
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/Narcissk.htm