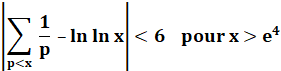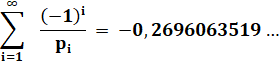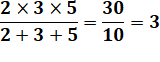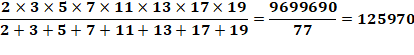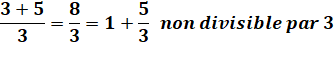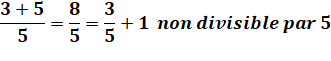|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Sommes et produits de nombres premiers Propriétés On connait la conjecture de
Goldbach: Tout nombre entier est la somme de trois nombres premiers et On connait moins la
propriété démontrée par Linnik: Tout entier suffisamment grand est la somme de deux premiers et au
plus k puissances de 2, k étant une constante. k = 1906 et même 200 en
admettant l'hypothèse
de Riemann. Cette page propose une étude
sur les propriétés générales de la somme des nombres premiers:
Un des résultats La somme de deux
produits de nombres premiers distincts n'est pas divisible par l'un de ces
premiers >>> Ex: (3 x 7) + (5 x 11) = 76 = 2 x 2 x 19 qui n'est pas divisible par (3, 7, 5 ou 11). |
|
La
somme de deux nombres premiers p et q est impaire. Que
dire de la divisibilité du produit p.q ? |
|
SOMME des nombres premiers
successifs |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Lecture: au rang 9, la somme de 2 + 3 + 5 + … + 23 =
100
Bilan: aucune formule
exacte pour calculer la somme de rang k.
Formule plus élaborée:
Observation: la somme cumulée est souvent composée, et
au moins un des facteurs est parmi les termes de la somme. Dit-autrement: la
somme cumulée et souvent divisible par un des premiers de la somme. Liste des sommes cumulées jusqu'au centième premier [2, 5, 10, 17, 28, 41, 58, 77, 100, 129, 160, 197, 238, 281, 328, 381, 440, 501, 568, 639, 712, 791,
874, 963, 1060, 1161, 1264, 1371, 1480, 1593, 1720, 1851, 1988, 2127, 2276,
2427, 2584, 2747, 2914, 3087, 3266, 3447, 3638, 3831, 4028, 4227, 4438, 4661,
4888, 5117, 5350, 5589, 5830, 6081, 6338,
6601, 6870, 7141, 7418, 7699,
7982, 8275, 8582, 8893,
9206, 9523, 9854, 10191, 10538, 10887, 11240, 11599, 11966, 12339, 12718,
13101, 13490, 13887, 14288, 14697, 15116, 15537, 15968, 16401, 16840, 17283,
17732, 18189, 18650, 19113, 19580, 20059, 20546, 21037, 21536, 22039, 22548, 23069, 23592,
24133] En jaune les nombres premiers; 100 est le
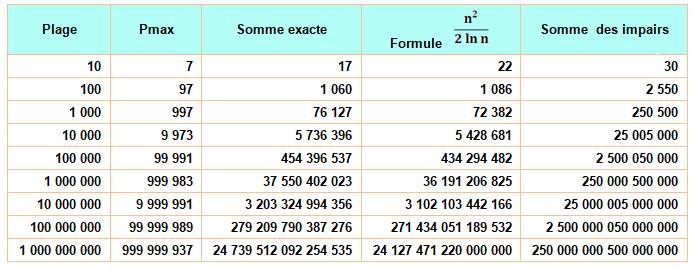
seul carré de cette liste; 4 888 est une curiosité de chiffres Sommes pour les plages en puissances de 10
La
formule simple conduit à une bonne approximation de la somme de premiers. La somme
des entiers impairs est citée à titre de borne supérieure de la somme des
premiers. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Valeur de p telle que la somme des premiers jusqu'à p et
divisible par p 2, 5, 71, 369119, 415074643,
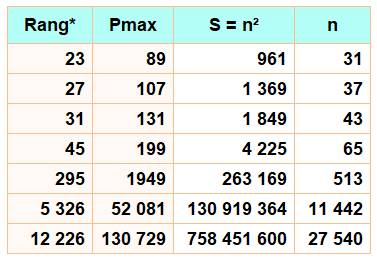
55691042365834801, ... OEIS A007506 Somme des premiers = Carrés (jusqu'au millionième premier)
Avec la somme des premiers impairs (tous sauf le 2) (Rang ou
quantité de termes dans la somme, ici sans le nombre 2, bien sûr)
Notez la
présence du nombre 23
dans les deux tableaux. Aucun cube = somme des premiers jusqu'au millionième premier Et un seul pour les
premiers impairs: 3 + 5 = 8 = 23 |
Voir Somme
des nombres premiers (Tables) / Formule de
la somme des entiers
Merci à Gérard Lopez pour ses contributions
|
|
||
|
La
divergence de cette série a été prouvée par Euler en
1737 pour la première fois (Diverses
observations relatives aux séries infinies). Sa démonstration originale (aves les produits d'Euler)
est considérée comme la base de la théorie analytique des nombres. Il disait: cette somme progresse vers l'infini
moins vite que la série
harmonique. Elle varie comme le logarithme de celle-ci. |
|
|
|
Somme alternée des inverses des nombres premiers |
|
|
Anglais: the
sum of the reciprocals of the prime numbers
Voir Programmation
– Index
Somme cumulée divisible par p ; par 100
|
Valeurs de p
telle que p divise la somme cumulée des nombres premiers jusqu'à p: 2, 5, 71, 369
119, 415 074 643 … Valeurs de p
telle que 100 divise la somme cumulée des nombres premiers jusqu'à p: 23, 563, 937, 2099, 3371, 5407, 6977
… |
|
|
||
|
Quels
sont les cas où la somme cumulée des nombres premiers divise le produit de
ces premiers (primorielle) |
Exemple avec k = 3 puis k = 8 nombres premiers
|
|
|
Liste des valeurs de k |
[1, 3, 8, 13, 23, 38, 39, 41, 43, 48, 50, 53, 56,
57, 58, 66, 68, 70, 73, 77, 84, 90, 94, 98, 126, 128, 134, 140, 143, 145, 149,
151, 153, 157, 160, 164, 167, 168, 172, 174, 176, 182, 191, 194, 196, 200,
210, 212, 215, 217, 218, 219, 222, 225, 228, 229, 231, 238, 264, 266, 267,
269, 272, 274, 278, 292, 293, 295, 299, 306, 310, 316, 318, 320, 323, 325,
333, 336, 340, 346, 351, 354, 360, 373, 384, 388, 393, 396, 402, 422, 424,
430, 448, 450, 454, 472, 476, 482, 493, 494, 497, 498, 500] |
|
|
Valeur des quotients |
1, 3, 125970, 1278362451795, 305565807424800745258151050335, 2099072522743338791053378243660769678400212601239922213271230,
330455532167461882998265688366895823334392289157931734871641555 … |
|
![]()
Somme de premiers et divisibilité
|
|
||
|
La somme de deux
nombres premiers est divisible par 2, sauf si l'un des premiers est le nombre
2. La somme de trois
nombres premiers est impaire, sauf si l'un des premiers est le nombre 2; elle
est alors paire et divisible par 2. D'une manière générale La somme de k nombres premiers est divisible par 2 si:
|
Somme de deux nombres premiers 3 + 5 = 8 = 2 x 4 divisible par 2 2 + 3 = 5 non divisible car présence du 2 Propriété qui résulte du fait que tous les nombres premiers sont
impairs, sauf 2; et que la somme de deux impairs
est paire. Somme de trois nombres premiers 3 + 5 + 7 = 15 2 + 3 + 5 = 10 = 2 x 5 En présence d'un 2, les deux autres sont impairs et ils produisent une
somme paire; la somme totale reste paire en y ajoutant le 2. |
|
Voir Table de sommes de premiers
|
|
||
|
Somme de deux premiers La somme de deux
nombres premiers n'est pas divisible par l'un des premiers de la somme. |
Exemples
Si l'un des termes de la somme est divisible par l'un des premiers,
l'autre ne l'est pas. En effet, les nombres premiers sont premiers entre eux et la division de
l'un par l'autre donne une fraction
irréductible. |
|
|
Somme de deux produits de premiers La somme de deux
produits de nombres premiers distincts n'est pas divisible par l'un des
premiers de la somme. |
Pour la même raison, chaque terme de la somme de deux premiers peut
être multiplié par des premiers distincts sans que la nouvelle somme soit
divisible par l'un de premiers. Un des termes produit toujours une fraction
non réductible car les nombres impliqués sont premiers entre eux.
|
|
|
Somme de trois premiers ou plus La somme de k
nombres premiers est souvent divisible par l'un des premiers de la somme. Comme le montre le tableau des sommes cumulées, la
somme de k premiers est souvent divisible par l'un d'entre eux. |
|
|
![]()
Exploration
|
|
||
|
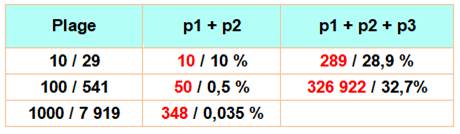
Taux de
formation d'un nombre premier avec la somme de deux premiers: Pour toutes les sommes des dix plus petits
premiers entre eux, soit de 2 à 29, il y a seulement 10
sommes qui sont premières, soit un taux de 10 %. Le taux de formation de sommes premières passe à
28,9 % avec trois nombres premiers. Bilan: une somme de
nombres premiers peut être première sans que ce soit la majorité des cas. |
La somme de deux nombres premiers est rarement un nombre premier.
Seulement 348 sommes premières sur un million
de sommes (0,35 pour 1000) pour les mille premiers nombres premiers (soit
jusqu'à p1 = 7 919 et p2 = 7 919). |
|
|
|
||
|
On
cherche à savoir si une combinaison de nombres premiers est riche de nombres
premiers. On part
du constat que la somme de deux produits de premiers n'est pas divisible par
l'un d'eux; sans doute propice à la production de nouveaux nombres
premiers. |
Exemples 2 x 3 + 5 = 11 premier 2 x 3 + 7 = 13 premier 3 x 5 + 7 = 22 = 2 x 11 |
|
|
Quelle
est la proportion de nombres premiers ainsi engendrés ? |
Pour p1.p2 + p3 Exemple avec les premiers < 10: avec toutes les possibilités de sommes distinctes (ST = 12), il y a SP
= 9 sommes premières, soit un taux de 75%. |
|
|
Somme de produits Plage => SP / ST, taux |
Exemples de telles sommes composées p1, p2, p3,
S, F = facteurs |
|
p1.p2 + p3 p < 10 => 9 / 12, 75 % p < 20 => 35 / 168, 20,8 % p < 50 => 102 / 1 365, 7,5 % p < 100 => 247 / 6 900, 3,6 % |
2, 3, 5, 11, F =
(11) 2, 3, 7, 13, F =
(13) 2, 5, 3, 13, F =
(13) 2, 5, 7, 17, F =
(17) 2, 7, 3, 17, F =
(17) 2, 7, 5, 19, F =
(19) 3, 5, 2, 17, F =
(17) 3, 5, 7, 22, F =
(2)(11) 3, 7, 2, 23, F =
(23) 3, 7, 5, 26, F =
(2)(13) 5, 7, 2, 37, F = (37) 5, 7, 3, 38, F = (2)(19) |
|
p1.p2.p3 + p4 p < 10 => 4 / 4, 100% p < 20 => 69 / 280, 24,6 % p < 50 => 423 / 5 460, 7,7 % p < 100 => 1 733 / 50 600, 3,42% |
2, 3, 5, 7, 37, F
= (37) 2, 3, 7, 5, 47, F
= (47) 2, 5, 7, 3, 73, F
= (73) 3, 5, 7, 2, 107, F = (107) … 3, 5, 7, 2, 107,
F = (107) 3, 5, 7, 11, 116,
F = (2)^2 (29) 3, 5, 7, 13, 118,
F = (2)(59) 3, 5, 7, 17, 122,
F = (2)(61) 3, 5, 7, 19, 124,
F = (2)^2(31) 3, 5, 11, 2, 167,
F = (167) 3, 5, 11, 7, 172,
F = (2)^2(43) 3, 5, 11, 13,
178, F = (2)(89) 3, 5, 11, 17,
182, F = (2)(7)(13) 3, 5, 11, 19, 184, F = (2)^3(23) 3, 5, 13, 2, 197, F = (197) |
|
p1.p2 + p3.p4 p < 10 = 3 / 3, 100% p < 20 => 54 / 210, 25,7% p < 50 => 366 / 4 095, 8,9 % p < 100 => 1 512 / 37 950, 3,98% |
2, 3, 5, 7, 41, F
= (41) 2, 5, 3, 7, 31, F
= (31) 2, 7, 3, 5, 29, F = (29) … 3, 5, 7, 11, 92,
F = (2)^2(23) 3, 5, 7, 13, 106,
F = (2)(53) 3, 5, 7, 17, 134,
F = (2)(67) 3, 5, 7, 19, 148,
F = (2)^2(37) 3, 5, 11, 13,
158, F = (2)(79) 3, 5, 11, 17,
202, F = (2)(101) 3, 5, 11, 19,
224, F = (2)^5(7) 3, 5, 13, 17,
236, F = (2)^2(59) 3, 5, 13, 19,
262, F = (2)(131) 3, 5, 17, 19,
338, F = (2)(13)^2 |
|
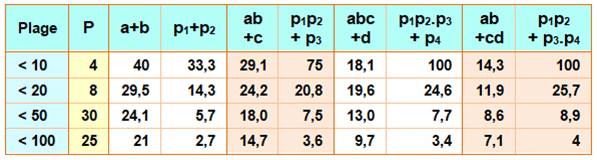
Bilan |
Le
tableau présente les statistiques de sommes premières selon que les nombres
dans l'opération sont quelconques (a,b,c,d) ou premiers (pi).
La
présence de nombres premiers dans ces sommes de produits n'est pas plus
propice à engendrer des sommes premières. C'est plutôt le contraire lorsque
la plage grandit. |
Merci à Louis
R. pour toutes ses suggestions
|
Question La
somme de deux nombres premiers p et q est impaire. Que
dire de la divisibilité du produit p.q ? Réponse Tous
les nombres premiers sont impairs (sinon, ils seraient divisibles par 2),
sauf justement 2. Une
somme de deux premiers est impaire seulement dans le cas d'un premier et du
nombre 2 (disons: p = 2). Alors p.q = 2q qui est divisible par 2. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()