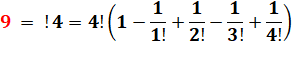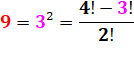|
Édition du: 06/05/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Nombre 9 |
||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
8 et 9 sont les seuls nombres puissants
consécutifs. Conjecture
de Catalan |
Propriété
majeure Le
nombre 9 (qui est aussi un chiffre) est remarquable par ses nombreuses
propriétés face à la divisibilité. La somme des chiffres
d'un nombre divisible par 9 est également divisible par 9 >>> Sum of all digits of a number divisible by 9 is also divisible by 9. |
|||
|
Voir Partitions |
||||
|
|
|
Préfixes
diviseurs et multiplicateurs: 10-9 nano 10 9 giga Voir |
||
Rappel
Propriétés générales >>>

Célèbre jeu qui consiste
à reconstituer les nombres avec k fois le
même chiffre
Ici, les nombres de 1 à
12 avec trois 9 au maximum
Voir Horloge / Horloges avec
indications mathématiques
Nombre
moins la somme des chiffres = 9
Voir Propriété
générale / Magie
du 9
|
Une
jeune poulette rentrant de l'école, annonce son exploit de la journée: Maman,
j'ai eu un 9. |
|
Un
boxeur insomniaque cherche une solution, sinon il perd ses matches. Pas de
chimie sinon dopage ! Alors son médecin lui conseille sagement de faire comme
autrefois: compter les moutons. Une semaine se passe et il est à nouveau chez
le médecin: - Docteur, il va falloir trouver autre chose. Les moutons, ce
n’est pas possible: à chaque fois que j’arrive à 9,
je me relève… |
Voir Pensées & humour
![]()
Numération
– Chiffres – Dénombrement

Voir Notion
de chiffres / Zéro
|
9 |
|
||
|
9 |
|
||
|
|
|
||
|
9 =
(2 x 2 – 1) (2² – 2 + 1) = 8 x 1 + 1 |
|
||
|
9 =
2 x 22 + 1 |
|||
|
xy + x + y ne donne
jamais 9 |
|||
|
1, 2, 3, 4, 5, 6, 7, 8, 9 9 divise 123456789 9 divise 987654321 9 divise 135792468, etc. |
|
||
|
9, 19, 9, 52 Cycle: 9, 28, 14,
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10,
5, 16, 8, 4, 2, 1 |
|
||
Diagramme de Ferrers du nombre 9

Voir Diagramme
de Ferrers
|
9 =
4 + 5 = 3 + 6 = 2 + 7 = 1 + 8 = 3 + 3 + 3 = … |
|
|
9 + 9 = 18 9 x 9 = 81 |
|
|
9 = 1 + 1 + 1 + 3 + 3 = 1 x 1 x 1 x 3
x 3 |
|
|
9 = 4 + 5 = 2 + 3 + 4 = 3² |
|
|
9 =
4 + 5 et 4 x 5 = 20 |
|
|
9 =
5 + 4 = 3 x 3 |
|
|
9
= 1 + 2 + 6 = 1 + 3 + 5 = 2 + 3
+ 4 |
|
|
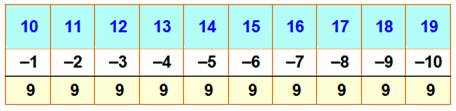
9
+ 10 + 11+ 12 = 13 + 14 + 15 |
|
|
9 = 2 + 2 + 5 = 3 + 3 + 3 |
|
|
9
= T2 + T3 = 3 + 6 = n² + 2n + 1 pour n = 2 |
Comme
tous les carrés |
![]()
Table
de multiplication du 9

Voir Table
complète
Voir Toutes les ASTUCES et CURIOSITÉS de
la multiplication par 9 et par 9…9
Multiplication transformée en
soustraction

Décalage de k crans car présence de k fois le 9
|
09
18 27 36
45 54
63 72 81
90 |
Rappel:
9 x 9 = 8 x 10 + 1 = 81 |
||||||||||
|
1233
=> 1+2+3+3 = 9 1233
= 9 x 137 (exemple) |
Preuve
par neuf. |
||||||||||
|
23 x 9 = 207 & 2 + 0 + 7 = 9 (exemple) |
|
||||||||||
|
(abc
– bca) / k 321 – 123 = 198 = 9 x 22 (exemple) 9 x 5 = 45
& 45 + 54 = 99 (exemple) |
|
||||||||||
|
9 =
(2+2) + (2-2) + (2x2) + (2/2) |
|||||||||||
|
d9 =
d + 9 + 9d 49 = 4 + 9 + 4 x 9 = 13 + 36 |
|
||||||||||
|
|
|
||||||||||
|
9 = n.m / (n + m) |
|
||||||||||
|
9 = 27 / 3 |
|
||||||||||
|
1 / 9 = 0,111… 2 / 9 = 0,222… 3 / 9 = 0,333… 4 / 9 = 0,444… 5 / 9 = 0,555… |
6 / 9 = 0,666… 7 / 9 = 0,777… 8 / 9 = 0,888… 9 / 9 = 1 |
|
|||||||||
|
a/9 =
0,aaa… ab/99 =
0,ababab…
|
On
montre cette propriété en utilisant cette relation:
On
poursuit en appliquant la même procédure à 1/90. |
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
7,
[9, 12] 9
= 3² et 10 = 2x5 => 10 – 3 = 7 |
Seul 12
partage cette propriété (n au moins jusqu'à 109). |
||||||||||
|
|
||||||||||
|
9 |
|
||||||||||
|
8n
– 7n
+ 6n – 5n + 4n – 3n + 2n
– 1n |
|
|
52 – 42
= 9 54 – 44
= 369 |
|
|
9 =
144 / 16 = 46 368 / 5 152 |
|
|
13 + 23 + 33 = 1
+ 8 + 27 = 36 = 9 x 4 23 + 33 + 43 = 8 + 27
+ 64 = 99 = 9 x 11 (exemples) |
Rappel
La barre verticale se lit "divise". |
|
9 |
|
|
9 ou produit
un reste de -1 ou 1 |
|
![]()
Sommes identiques des chiffres des
puissances
|
9 = 9 |
9 |
95
= 59049 |
5+9+0+4+9
= 27 |
|
92
= 81 |
8+1
= 9 |
98
= 43 046 721 |
4+3+0+4+6+7+2+1
= 27 |
|
93
= 729 |
7+2+9
= 18 |
97
= 4 782 969 |
4+7+8+2+9+6+9
= 45 |
|
94
= 6 561 |
6+5+6+1
= 18 |
99
= 387 420 489 |
3+8+7+4+2+0+4+8+9
= 45 |
|
96
= 531 441 |
5+3+1+4+4+1
= 18 |
910
= 3 486 784 401 |
3+4+8+6+7+8+4+4+0+1
= 45 |
Voir Tables
de telles relations
|
n² = ….x9 |
C'est vrai pour tous les autres chiffres
sauf 00 et 44. |
||
|
9 =
3² = 23 + 13 |
|
||
|
|
|
||
|
9 =
3² = 2² + 2² + 1² 2² = 4 = 1² + 1² + 1² + 1² 4² = 16 =
2² + 2² + 2² + 2² |
|
||
|
9 =
13 + 23 = 3 x 3 |
|
||
|
9 =
3² = 1 + 3 + 5 |
|
||
|
9
= 5
+ 4 =
5² – 4² |
|
||
|
9 = 5² – 4² = 3²
= 3² x 1²
|
|
||
|
29² = (30 – 1)² = 900 – 60 + 1 = 841 (exemple) |
|
||
|
… 9 = n² |
|
||
|
9 =
3² = 3² = 23 + 1 = 13 + 23
= (1 + 2)² |
Voir Carré d'un nombre
triangulaire égal somme de cubes
|
||
|
9 = 3² = 5² – 4² |
|
||
|
9 =
1² + 2 x 2² = 13 + 1 x 23 = 22 + 5 x 12 |
|
||
|
9 = 10 – 1² – 0² =
11 – 1² – 1² =
34 – 3² – 4² =
74 – 7² – 4² =
90 – 9² – 0² =
91 – 9² – 1² |
C'est le record. Voir Curiosité |
||
|
8 = 23 & 9 = 32 |
|
||
|
9
= (0)3 + 13 + 23 = 2173 + (–52)3 + (–216)3 = 20973
+ 113053 + (–11329)3 |
|
||
|
9 =
13 + 23 = 3 x 3 |
|
||
|
|
|
||
|
|
|
||
|
9 = 52 – 42 = 25 –
16
= 62 – 33 = 36 –
27
= 152 – 63 = 225 – 216 =
2532 – 403 = 64 009 – 64 000 |
|
||
|
92k = ... 1 92k+1 = ... 9 |
|
||
![]()
Nombre
en puissances

|
92 = 81 et 8 + 1 = 9 83 = 512 et 5 + 1 + 2 = 8 74 = 2401 et 2 + 4 + 0 +1 = 7 |
|
|
|
7² = 2² +
3² + 6² = 49 9² =
1² + 4² + 8² = (8 + 1)² = 81 11² = 2² +
6² + 9² = 121 |
Le plus
petit avec 7² et le suivant avec 11. |
|
|
9² = 81 => 8 + 1 = 9 = 3² 10² = 100 (1); 11² = 121 (4); 12² = 144 (9); 13² = 169 (16); 14² = 196 (16); 15² = 225 (9) |
Premier
tel nombre d'une suite de sept. |
|
|
|
|
|
|
9²
= 41² – 40² = 41 + 40 |
|
|
|
(9² +
10²)² = 1053 – 1043 = 32 761 |
|
|
|
92 – 1 =
80 93
– 1 = 728 = 8 x 91 |
|
|
|
|
|
|
|
93 = 729 = 8 x 9
x 10 + 9 =
720 + 9 = 729 |
|
|
|
93 = 13 + 63 + 83
= 23 + 23 + 33
+ 73 + 73 |
Les trois
seules pour jusqu'à cinq cubes dont |
|
|
9 cubes pour 23 et 239 |
Tout
nombre est la somme d'au plus neuf cubes. En fait, tous sont somme de huit
cubes sauf 23 et 239. |
|
|
94 = 93 + 183 |
|
|
|
94 = 24 + 44 + 64 + 64 + 64
+ 74 = 16 + 256 + 3x1296 + 2401 = 6 561 |
|
|
|
9, 81, |
L'unité
est 1 pour les puissances paires et 9 pour les impaires. |
|
|
92 = 81 94 = 6561 96 = 531 441 88 = 16 777 216 910
=
3 486 784 401 |
|
|
|
|
Liste: 1, 2,
3, 9, 18, 27, 54, 90, 108, 163, 197, 254, 432, 1292, 2202, 9648, … OEIS A108827 |
|
|
…u9 = … u |
|
|
|
9 9^9 = 9 387 420 489 = 42812477... ...27177289 = 4,281... 10369 693 099 |
||
|
29 + 9 = 521 |
|
|
![]()
Autour
du nombre
Joli motif avec les repdigits en 9

|
0, 1, 2 … 9 |
|
|
910 = 1003 |
|
|
1
ou 9 |
|
|
9 =
Sc{6!, 7!, 8! } |
|
|
9 =
!4 = 4! * (1-1/1!+1/2!-1/3!+1/4!) |
|
|
… 999 999 … |
|
|
(9 x 123 456 789) – 123 456 789 = 987 654 321 – 9 |
|
|
12
345 678 x 9 + 9 =
111 111 111 |
|
|
9 |
10 9+1 – 1 |
|
|
1 + 9 = 10 1 × 9 = 9
|
|
||||
|
|
|
||||
|
|
|
||||
|
= 9 x 14 941
(exemple) |
|
||||
|
9 = 3² = 65 – 56
et 65 + 56 = 11² |
|
||||
|
12 x 8 + 2 =
98 123 x 8 +
3 = 987 1234 x 8 +
4 = 9876 12345 x 8
+ 5 = 9876 … |
|
||||
|
12
x
9 + 3 = 111 123 x 9 +
4 = 1111 1234 x 9 +
5 = 11111 … |
|
||||
|
9 x
987654321 = 8 888 888 889 18
x
987654321 = 17 777 777 778 27 x
987654321 = 26 666 666 667 … |
|
||||
|
9
x 1089 = 9801 9
x 10089 = 90801 9
x 10449 = 94041 … |
|
||||
|
|
|
||||
Sommes des
puissances successives de 9
|
90 + 91 + 92 + … + 9k = …u ? 90 + 91 = 1 + 9 = 10 = …0 90 + 91 + 92 = 10 + 81
= …1 90 + 91 + 92 + 93
= …1 + …9 = …0 Les cinq premières sommes: [1, 10], [2, 91], [3, 820], [4, 7381], [5, 66430] |
L'unité
des puissances de 9 est 1 pour les puissances paires et 9
pour les impaires. L'unité de
la somme vaut: u = 1 si k
est impair, et u = 0 si k
est pair. La somme est
un nombre triangulaire. Voir Brève
22-431 |
|
|
N
= 91 + 92 + 93 + 94 = 7 380 = 2 x 3 690 |
Le nombre
9 est impair,
ses puissances sont impaires. La somme de quatre impairs est paire. |
|
|
9 =
1! + 2! + 3! |
|
|
|
9 x 2 = 18
& 1 + 8 = 9 99
x 2 = 198 & 1 + 98 = 99 |
|
|
|
9 = 97524 / 10836
= 95823 / 10647 |
|
|
|
9 x 16 583 742 = 149 253 678 9 x 26 x 531 487 = 627 x 198 354 = 124
367 958 |
|
|
|
9 =
4 / 0,444…. |
|
|
Suite
Géométrie, Jeux, Culture …
Décimales
Voir page dédiée >>>
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
|
|
2, [1, 0, 0, 1] 3, [1, 0, 0] 4,
[2, 1] 5,
[1, 4] |
6,
[1, 3] 7,
[1, 2] 8, [1, 1] 9,
[1, 0] |
8,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()
Âge deviné >>>
Magie >>>
Nombre Irrationnel >>>