NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/07/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	PENTAGONES				Glossaire Géométrie
INDEX Polygones Constructions Géométrie Énigmes	Général	Données	Constructions
	Pentagone	Mesures	Méthodes générales	Cercles – Mascheroni
	Nombre d'or	Angles	Avec Racine de 5	Approchée de Dürer
	Pentacle	Segments	Avec bissectrices	Approchée originale
	Pavage	Énigmes	Méthode Euclide	Dissection
	Aire à partir de ses triangles		Meccano
	Sommaire de cette page >>> Cornet de glace >>> Triangles dans pentagone >>> Pentagone et triangle isocèle

Énigmes avec le PENTAGONE

Problèmes de calcul de longueurs ou d'angle au sein du pentagone régulier.

Cornet de glace
Énigme Un cornet de glace avec fraise, vanille et fraise. La section plane montre un triangle isocèle surmonté d'un pentagone régulier. Quelle est la plus grande surface: la rose ou la jaune ? Solution Les triangles roses (1 et 2) se retrouvent dans la partie jaune. L'aire rose est égale à l'aire jaune. Explications Les côtés des triangles CDE et FBC sont égaux deux à deux. Les deux triangles sont égaux (superposables). Les angles BAF et ECF valent 36°. BF = FE = côté du pentagone. Les triangles isocèles ABF et CFE, avec un côté égal et l'angle au sommet égal, sont égaux.

Voir Brève 685

Triangles dans pentagone
Énigme Un pentagone régulier. Un triangle équilatéral posé sur un côté du pentagone. Quelle est la valeur de l'angle formé par des deux segments figurés en vert ? Solution Le pentagone et le triangle ont des côtés de même longueur d'où la création de triangles isocèles. Dans un triangle isocèle, l'angle à la base vaut la moitié de 360° diminué de l'angle au sommet.

Voir Brève 686

Pentagone et triangle isocèle
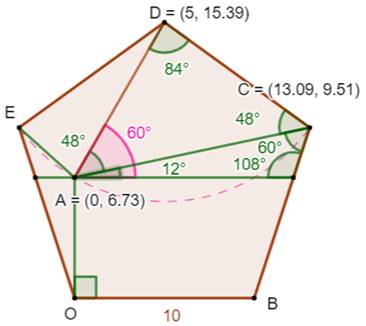
Énigme Un pentagone régulier. Une verticale. Un cercle qui coupe la verticale. Montrez que l'angle indiqué vaut bien 48°. Solution La solution ne semble pas simple ! On peut calculer les longueurs et les angles et arriver progressivement à cet angle. Une autre solution consiste à passer en analytique (équations).

Solution analytique Voir la figure annotée construite avec GeoGebra. Procédure suivie: Coordonnées des points C, D; Celles du point A par intersection avec le cercle; et Calculs de la pente des droites AC et AD La différence sera la valeur de l'angle cherché. Les calculs sont effectués avec un pentagone de côté unité (multipliez les longueurs trouvées par 10 pour trouver celles de la figure).
Point C
Point D
Équation du cercle
Point A (x = 0) L'une des racines de l'équation.
Pente AC (calcul pas simple)
Pente AD
Angle CAD recherché	60 – 12 = 48°

Solution par calculs géométriques Voir le site indiqué

La solution fait usage de la loi des sinus et la loi des cosinus dans les triangles.

Retour	Pentagone – Généralités
Suite	Angles du pentagone Centre de gravité du pentagone Construction étonnante du pentagone Pentagone et le nombre d'or Pentagones de Dürer Hexagone
Voir	Calcul de Pi Construction géométrique des nombres Dodécagone Géométrie – Index Pentagone et racines de 1 Polygone Partage du cercle en parts égales Pavage avec polygones Hexagone – Généralités
Site	Pentagon and Equilateral Triangle – eyleMMath Isosceles in a pentagon – eyleMMath
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/PentaEni.htm