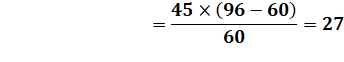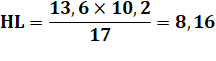triangle rectangle - exercices en quatrième

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/05/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	TRIANGLES et CARRÉS Exercices					Glossaire Triangle
INDEX Triangle Géométrie Jeux et énigmes Collèges	Types	Rectangle		Isocèle	Équilatéral
		Quatre carrés		Tête géométrique	Carré et 2 Trg Équilatéraux
		Exercices 01		Escalier dans cercle	Rect et 2Trg Équilatéraux
				Carrés dans cercle	Triangle dans le cercle
	Quatrième		Sommaire de cette page >>> Exercice 01 >>> Exercice 02 >>> Exercice 03 >>> Exercice 04

Exercice 01

Énoncé

Un parc rectangulaire ABCD:

Longueur: BC = 96 m;

Largeur: AB = 45 m.

Elsa en E veut rejoindre Bruno en B en ligne droite. En croisant AD, le bord du parc, elle note que AF = 60 m.

Elle se demande quelle est la distance qu'elle a parcourue.

Aperçu avec GeoGebra

Le dessin de la figure à l'échelle montre que BE = 12 cm à l'échelle 1/10; soit la longueur réelle: 120 m.

Pour connaitre cette valeur, la figure terminée, dessinez le segment BE et lisez sa longueur dans la fenêtre de gauche.

Résolution

Théorème de Pythagore

On remarque que l'on connait AB = 45 et AF = 60 dans le triangle rectangle ABF.

BF² = AB² + AF² = 45² + 60² = 5 625 = 75²

BF = 75 m

Théorème de Thalès

Avec les triangles rectangles FAB et FDE.

Théorème de Pythagore

Dans le triangle rectangle BCE.

BE² = BC² + CE² = 96² + (45 + 27)² = 14 400

BE = 120

Exercice 02
Énoncé Un triangle isocèle ABC. Base: AB = 6 m; Hauteur: CI = 3,5 m. Un rectangle interne EFGH. Largeur: EG =2,1 m. Quelle est sa longueur: GH = ?
Aperçu avec GeoGebra Le dessin de la figure à l'échelle 1/100^e montre que GH = 2 x 1,2 = 2,4 m. Note: GeoGebra est simple et gratuit. Il est utilisé dans les collèges et les lycées
Résolution On considère les triangles rectangles CDF et CIB. On connait leur rapport d'homothétie (de grossissement).
Théorème de Thalès Le même rapport s'applique à l'autre côté des triangles rectangles.	Et GH = EF = 2DF = 2,4 m

Exercice 3

Avec cette figure:

1. Calculez la longueur du segment NE.

2. Montrer que l'aire du triangle NOE est égale à celle du triangle NEL.

Exercice 3 – Solution
Réponse en figure Explications
La longueur de NE se calcule facilement avec le théorème de Pythagore.	NE² = NO² + OE²
LH une la hauteur du triangle quelconque NEL. L'aire du triangle est égale à la moitié du produit d'un côté* par la hauteur qui lui correspond.	A_NEL = ½ (NE . HL)
Le triangle NOE est un triangle rectangle. Son aire est égale à la moitié de celle du rectangle. Ou encore, avec NO comme base et OE comme hauteur; ou encore avec OE comme base et NO comme hauteur.	A_NOE = ½ (NO . OE)
Le calcul des aires montrent qu'il y a égalité:	A_NEL = A_NOE = 69,96 m²

* Il faudrait, chaque fois, dire: la longueur d'un côté ou la mesure d'un côté.

Certes, mais dit-on "boire un verre" ou "boire le contenu d'un verre".

Il est vrai qu'en maths, il faut être précis, du moins, éviter les confusions possibles.

Remarque 1 (Fondamental à savoir en 4^ème)

Le point L est indéterminé. On peut mettre HL n'importe où. Même H en E ou même en N. L'aire du triangle NEL sera toujours la même.

A_NEL = ½ (NE . HL)

Remarque 2 (Pour se prouver qu'on a bien compris)

On faire la démonstration à l'envers: quelle est la valeur de HL pour que les deux triangles aient la même aire A? Nommons les deux côtés x = NO et y = OE.

Application numérique à notre cas:

Conséquence: l''énoncé aurait pu proposer toutes valeurs de x et y et donner la mesure de HL selon la formule trouvée. Un triplet de Pythagore sous la racine serait le bienvenu pour donner une valeur entière.

Avec le triplet classique 3² + 4² = 5², la valeur de HL serait égale à 2,4.

Remarque 3 (Pour élève curieux)

On peut aussi vérifier que les calculs " tombent justes". On cherche les produits qui donnent les nombres donnés dans l'énoncé. Pour avoir des entiers, on multiplie tout par 100, ce qui ne change rien (Au lieu de mètres, on a des centimètres).
Rappel: 2⁴ = 2x2x2x2 = 16

1 360 = 2⁴ . 5 . 17

1 020 = 2² . 3 . 5 . 17

1 700 = 2² . 5² . 17

La fraction se simplifie pour donner la mesure attendue.

Remarque 4 (Hors programme de 4^ème)

Dans le calcul de NE = 1700 se cache un célèbre triplet de Pythagore qui permet d'obtenir une racine entière.

Voir Facteurs / Puissances

Exercice 04
Étant donné a et b, calculer c, h et d. Applications numérique avec a = 12 et b = 20.
a = 12, c = 16 et b = 20 h = 21, a+c = 28 et d = 35 Voir Théorème de Thalès
Autres configurations de deux triangles de Pythagore semblables. Le premier exemple (jaune) est celui traité ci-dessus. Toutes les valeurs pour a de 1 à 100 et b de 1 à 150.	a, c, b, h, a+c, d 12, 16, 20, 21, 28, 35 24, 18, 30, 56, 42, 70 24, 32, 40, 42, 56, 70 36, 27, 45, 84, 63, 105 36, 48, 60, 63, 84, 105 48, 36, 60, 112, 84, 140 48, 64, 80, 84, 112, 140 60, 25, 65, 204, 85, 221 60, 45, 75, 140, 105, 175 60, 80, 100, 105, 140, 175 72, 54, 90, 168, 126, 210 72, 96, 120, 126, 168, 210 84, 63, 105, 196, 147, 245 84, 112, 140, 147, 196, 245 96, 72, 120, 224, 168, 280