NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités					Glossaire Triangle
INDEX Types de triangles Triangle Polygones	Point Milieu	Droites et points	Pappus		Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli		Triangles et triangles
	Triangulation	Quatre triangles	Heilbron		Carrés triangles
		Représentation	Brocard		Cercles et triangles
		Triangles dans les polygones		Régions et intersections
	Sommaire de cette page >>> Approche >>> Triangles et carrés >>> Théorème et démonstration >>> Triangulation

Triangulation des POLYGONES

Dans un polygone à n côtés, on dispose p points.

Le polygone contiendra 2p + n – 2 triangles.

Voir Noms des polygones / Principe de la triangulation

Approche
Étant donné un polygone à n côté et p points internes, le principe de la triangulation consiste à partager le polygone en autant de triangles que possible, sans croisement. Sur la figure, avec un quadrilatère et quatre points internes, on peut composer dix triangles. Comment établir une formule donnant la quantité de triangles (q) en fonction du nombre de sommets (n) et de la quantité de points internes (p).

Triangles et carrés
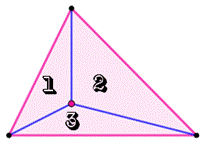
Dans le triangle, avec: 1 point: 3 triangles internes 2 points: 5 3 points: 7 4 points: 9 (+2 pour un nouveau point) … p points: 2p + 1
Dans le quadrilatère, avec: 1 point : 4 triangles 2 points: 4 + 2 = 6 3 points: 6 + 2 = 8 … p points: 2p + 2

Théorème
Avec un polygone quleconque de n côté et p points internes, on peut former exactement: q = 2p + (n – 2) triangles.	Propriété invoquée La somme des angles d'un polygone est égale à 180° (n – 2). Celle du triangle est 180°.
Démonstration Supposons que la formule doit juste. LA somme de tous les angles des triangles vaut	180 (2p + n – 2) = 360p + 180 (n-2)
Somme des angles autour des points internes	360 p
Somme des angles des triangles sans la contribution des angles internes.	360p + 180 (n-2) – 360p = 180 (n – 2)
Cette valeur est précisément celle des angles du quadrilatère	La formule est validée.

Voir Brève 607

Triangulation
Un moyen de compter les triangles consiste à les repérer par un numéro ou un point. Si le compte ne correspond pas à la formule, revérifiez. Méfiez-vous des alignements.

Suite	Principe de la triangulation Régions et intersections dans les polygones Compter les triangles dans une figure quelconque Devinette avec deux triangles Segments dans une grille Droites passant par n point sur une grille
Voir	Carré dans le triangle, construction astucieuse Dénombrement – Index DicoMot Géométrie – Index Heptagone et ses diagonales Jeux et puzzles – Index Nombres triangulaires Polygones – Index Triangle – Index
Sites	Triangulation d'un polygone – Wikipédia Triangulation – Christian Nguyen – pdf 35 pages Triangulation de polygones – Diagrammes de Voronoï et Triangulation de Delaunay – Achraf Othman – pdf 50 pages
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Triangul.htm