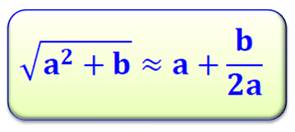NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/12/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 31

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

600. Amusement avec deux dés
Demandez à quelqu'un de faire les opérations indiquées et dîtes-lui que vous pouvez deviner son résultat. Vous lui répondez 49 ! En effet, les opérations sont telles que la valeur des dés s'éliminent en remarquant que la somme des valeurs sur deux faces opposées est toujours 7.
Brèves associées	>>> Nombres deviné – Magie	>>> Brèves Magie – Index
Pour en savoir plus	>>> Nombre 49	>>> Jeu de dés >>> Magie – Index

601. Preuve par 9
Racine numérique La racine numérique (RC) d'un nombre est la somme de ses chiffres, éventuellement répétée pour aboutir à un seul chiffre. Exemple de calcul de RC RC (123 456 789) => 1+2 = 3 3+3 = 6 6+4 = 10 => 1 1+5 = 6 6+6 = 12 => 3 3+7 = 10 => 1 1+8 = 9 9 + 9 = 18 => 9 Le nombre 123 456 789 est divisible par 9. La division ne s'impose que si l'on veut connaitre la quotient (13 717 421). Remarque Dans ce système où on cherche la divisibilité par neuf, le 9 est équivalent à 0. En effet, le 9 est divisible par 9 avec 0 pour reste.		Propriété RC du résultat d'une opération = Résultat du calcul avec les RC. Preuve par 9 d'une multiplication À gauche la multiplication et à droite la même multiplication, mais avec les RC. Divisibilité par 9 Si on soustrait ses chiffres à un nombre, le résultat est toujours divisible par 9.
Brèves associées	>>> Nombre 9 – Multiplication >>>		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Preuve par neuf		>>> Nombre 9

602. Nombres croissants et preuve par 9

La somme des chiffres d'un nombre croissant (chiffres consécutifs) multiplié par 9 est égale précisément à 9.

Explication

9 x abcde avec a < b < c < d < e

Cela revient à multiplier par 10 – 1. Soit l'opération:

a	b	c	d	e	0
–	a	b	c	d	e

Qui, du fait que les nombres sont croissants, s'écrit:

a + (b-a) + (c–b) + (d-c) + (e-d-1) + (10-e) = 9

Cette simplification des termes deux à deux se nomment simplification par télescopage.

12 x 9 = 108 => RN = 9

123 x 9 = 1 107 => RN = 9

1 234 x 9 = 11 103 => RN = 9

12 345 x 9 = 111 105 => RN = 9

45 x 9 = 405 => RN = 9

456 x 9 = 4 104 => RN = 9

4 567 x 9 = 41 103 => RN = 9

13 579 x 9 = 122 211 => RN = 9

2 468 x 9 = 22 212 => RN = 9

1 234 56 789 x 9 = 1 111 111 101 => RN = 9

Plus petit et plus grand nombres tels que la multiplication par 9 présente un chiffre k donné.

Seuls quatre cas avec 8:

2 x 9 = 18 => plus petit

9 x 9 = 81

12 x 9 = 108

89 x 9 = 801 => plus grand

Plus k décroit et plus la quantité de cas croit. Pour k = 1, il y a 470 nombres croissants: 2, 12, 13, 123, 14, 24, 124 …

Brèves associées

>>> Nombres pannumériques

>>> Brèves Opérations – Index

Pour en savoir plus

>>> Preuve par neuf

>>> Nombres croissants

603. Glace 2 boules, 3 parfums

Quantité de compositions possibles

11 – Fraise, fraise 22 – Vanille, vanille 33 – Chocolat, chocolat 12 – Fraise, Vanille 13 – Fraise Chocolat 23 – Vanille Chocolat

6 possibilités

Formule de calcul

n parfums k boules

Calcul

Brèves associées

>>> Tirage des boules

>>> Brèves Dénombrement – Index

Pour en savoir plus

>>> Choix k parmi n avec répétition

>>> Combinaisons

604. Le verre penché – Énigme
Verre ballon demi-sphérique à moitié plein. De quel l'angle maximum peut-on le pencher sans verser une goutte de liquide ? Cet angle vaut 30°. En effet, le complémentaire de l'angle marqué en vert a pour cosinus (1/2 R / R = 1/2), ce qui correspond à un angle de 60°.
Brèves associées	>>> Trois verres et dix pièces		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes avec des verres		>>> Sphère

605. Constante de Gelfond

Nombre réel transcendant (non racine d'une équation polynomiale).

Transcendance démontrée en 1929 par Alexandre Gelfond (russe: 1906-1968).

Il s'agir de deux nombres irrationnels avec une opération qui les relie aux nombres imaginaires.

Cette relation résulte directement de l'identité d'Euler.

Curiosité: presque entier !

	Identité d'Euler
	Constante de Gelfond = 23, 140 692 64...
	= 0, 207 879 576...

Brèves associées

>>> Un à la puissance i (imaginaire)

>>> Brèves Nombres – Index

Pour en savoir plus

>>> Exponenteille et imaginaire

>>> Puissance de l'imaginaire

>>> Théorème de Gelfond

606. Premiers retournés - EMIRP
Un nombre EMIRP: premier en anglais – prime – épelés à l'envers. Ce sont des nombres premiers qui restent premiers en les retournant, comme 13 et 31. Sont exclus les nombres uniformes (repdigits) comme 11 ou 999. Il y a mieux. Par exemple: 1193 et 3911 sont EMIRP. Mais aussi une majorité de leurs permutations: 1931, 9311, 3119, 1319, 1913 et 3191.		Liste jusqu'à 1000 13, 17, 31, 37, 71, 73, 79, 97, 107, 113, 149, 157, 167, 179, 199, 311, 337, 347, 359, 389, 701, 709, 733, 739, 743, 751, 761, 769, 907, 937, 941, 953, 967, 971, 983, 991. Chacun se retrouve répété avec son retourné (exemples en rouge).
Brèves associées	>>> Premiers et somme de chiffres		>>> Brèves Premiers – Index
Pour en savoir plus	>>> EMIRP		>>> Nombrs premiers permutables

607. Triangulation des polygones
Théorème Avec un polygone quelconque de n côté et p points internes, on peut former exactement: q = 2p + (n – 2) triangles. Carré et quatre points q = 2x4 + 4 – 2 = 10 triangles. Impossible de faire moins; impossible de faire plus !		Ce carré est partagé en dix triangles
Brèves associées	>>> Triangle – Partage en k parts égales		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangulation des polygones		>>> Triangulation

608. Rébus mathématique
Résoudre ce rébus mathématique !
Le logarithme d'une exponentielle redonne le nombre lui-même. La racine cinquième d'une puissance cinquième redonne le nombre lui-même. Cette intégrale en dx est égale à la différence entre ses bornes.			I love math and physics J'aime les maths et la physique
Brèves associées	>>> Énigme du parking			>>> Brèves Jeux – Index
Pour en savoir plus	>>> Rébus >>> Racines			>>> Logarithmes >>> Intégration

609. Racine carrée approchée
Formule pour approcher une racine carrée.		Exemples pour: 7,0710… pour: 10,2469…
Brèves associées	>>> Calcul mental du carré		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Racine carrée		>>> Racine carrée – Index

610. Sinus et cosinus et puissance 4
Calcul qui montre que cette différence en puissance 4 et la même qu'en puissance 2. Utilisation de l'identité remarquable (ligne 3): a² – b² = (a – b) (a + b)		Exemple: cos^4 (60°) – sin^4 (60°) = cos (120°) = -1/2
Brèves associées	>>> Sinus et cosinus & DEMI		>>> Brèves Trigonométrie – Index
Pour en savoir plus	>>> Relations trigonométriques >>> Trigonométrie – Index		>>> Identités remarquables

611. Repdigit et 37
Ces fractions amusantes s'expliquent du fait que 111 = 3 x 37
Brèves associées	>>> Nombre 3 367	>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 37 >>> Nombre 111	>>> Repdigits >>> Pépites numériques

612. Division rapide par 99
Exemple de division 456789 / 99 = ? Bilan 456789 / 99 = 4614 reste 3 = 4614,030303…		La division par 99 est très simple: Partager le nombre en blocs de 2 chiffres à partir de la droite (45 67 89). Ajouter le bloc suivant à la somme complète obtenue (45 + 67 = 112 => 12 et 1 de retenue). Les retenues sont abaissées (1 en dessous du 45). Le reste est réalisé avec la somme finale (bloc dizaine-unité + centaine). Ici: 01 + 2 = 3. Le résultat est: soit euclidien quotient: 4614 et reste 3. soit décimal (périodique): 4614,030303… Le surlignement (colonne de gauche) indique que la période se répète à l'infini.
Brèves associées	>>> Division par 91		>>> Brèves Calcul mental – Index
Pour en savoir plus	>>> Division rapide par 99 >>> Nombre 99		>>> Division rapide par 9 >>> Calcul mental – Index

613. Plus petit nombre insignifiant
Tous les nombres ou presque possèdent une caractéristique propre. Exemple avec les nombres de 0 à 10 => Existe-t-il un nombre sans propriété particulière, un nombre insignifiant ? Si oui, ce nombre devient particulier en ce sens qu'il est le plus petit insignifiant et, de ce fait, rentre dans la liste des nombres ayant une propriété. Avec l'engouement pour les nombres, on ne retient plus l'inventivité des mathématiciens et amateurs de nombres pour trouver de nouvelles propriétés, réduisant à néant le champ des insignifiants.		Une propriété saillante pour chaque nombre 0 – Élément neutre de l'addition. 1 – Élément neutre de la multiplication. 2 – Seul nombre premier pair. 3 – Plus premier impair. 4 – Plus petit carré (non trivial). 5 – Toutes ses puissances se terminent par 5. 6 – Factorielle de 3: 1x2x3 = 6 = 3!. 7 – Plus petit nombre de Mersenne premier. 8 – Seul cas de puissances consécutives: 8 = 2^3 et 9 = 3^2. 9 – Divisibilité par 9: la somme des chiffres est divisible par 9. 10 – Base de notre système de numération.
Brèves associées	>>> Nombre 0 et nombre 1		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Empreinte des nombres >>> Tous les types de nombres		>>> DicNombre

614. Puissance n^0 = 1
Théorème Tout nombre à la puissance 0 est égal à 1. Commentaires La fraction n / n est posée. Elle vaut 1. On sait que n = n^1et que 1/n = n^-1. Avec un produit de puissances, les exposants s'ajoutent: n^1 . n^-1 = n^1 – 1 = n^0 Exemples 3^0 =2^0 = 1^0 = 0^0 = (–1)^0 = (–2)^0 = 1 Notez que: – 2^0 = – (2^0) = –1
Brèves associées	>>> Puissances négatives de 2		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Puissance 0 >>> Puissances négatives		>>> Nombre 0

615. Fraction continue à la demande
Fraction continue de la racine de 2021 avec 2020 pour numérateur. Comment s'y prendre ? Méthode Toute racine peut s'écrire comme ceci: En remplaçant racine de n par sa valeur: On recommence autant de fois que l'on veut. Pour 2021, on a choisit a = 1.		Calcul On exécute un premier calcul en remplaçant racine de n par une valeur approchée, disons 44 pour 2021. Les calculs suivants sont réalisés en injectant le résultat du calcul précédent à la place de racine de n. Formule pour le fun, car la convergence n'est pas très rapide.
La fraction continue conventionnelle avec 1 pour numérateur est: [44, 1, 21, 2, 21, 1, 88, 1, 21, 2, 21, 1, 88, 1, 21, …]
Brèves associées	>>> Fraction – Construction géométrique			>>> Brèves Calculs – Index
Pour en savoir plus	>>> Fractons continues			>>> Nombre 2021

616. Spirale en racines carrées
La construction du nombre racine de 2 est bien connue: c'est la longueur de la diagonale du carré unité. Avec cette construction comme point de départ, il est possible de construire la racine de 3 en traçant la perpendiculaire à la diagonale et en y reportant une longueur unité. La nouvelle diagonale mesure racine de 3. Ainsi de suite. La figure est la spirale de Théodore de Cyrène ou l'escargot de Pythagore. En 1958, Erich Teuffel a démontré que les rayons ne se superposent jamais.
Brèves associées	>>> Racine de n – Const. géométrique		>>> Brèves Constructions – Index
Pour en savoir plus	>>> Spirale de Théodore de Cyrène		>>> Racines carrées

617. Formulaire du cercle
Brèves associées	>>> Cercle – Rayon et cordes sécantes	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aires secteur, segment …	>>> Cercle – Index

618. Équation B.A^B = B^X
Résoudre: 9^3 + 9^3 + 9^3 = 3^xSolution: 3 x (3²)^3 = 3^x 3^1 x 3^6 = 3^x 3^7 = 3^x x = 7 Généralisation Résoudre: B . A^B = B^X Une trentaine de solutions pour A et B jusqu'à 100.		Solutions pour A et B inférieurs à 10
Brèves associées	>>> Équations et Racines – Un bon truc!		>>> Brèves Équations – Index
Pour en savoir plus	>>> Nombres ABA		>>> Équations

619. Point de Feynman et Pi
Décimales de Pi On s'intéresse à la répétition des décimales dans la constante Pi. Exemple: la première répétition de deux chiffres se trouve à la 24^e décimale avec 33. 3,1415926535 8979323846 26433832795 On trouve ensuite 88 en 34^e position.		Point de Feynman La première occurrence de six répétitions intervient à la position 762, dite point de Feynman, avec 999 999. Il faut dépasser la cent-millième position pour trouver l'occurrence suivante. Occurrences de six chiffres identiques dans Pi [Rang, valeur des sic décimales] [762, 9], [193034, 9], [222299, 8], [244453, 5], [252499, 6], [253209, 5], [255945, 1], [399579, 7], [419997, 5], [452071, 7], [710100, 3], [710101, 3], [828499, 4], [963024, 2],…
Brèves associées	>>> Constante Pi – Formules		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Nombres ABA		>>> Équations

Retour	Brèves de maths – Page 30
Suite	Brèves de maths – Page 32
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve31.htm