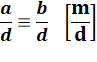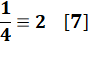Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 24/09/2020 M'écrire Brèves de Maths

INDEX Théorie des nombres Types de nombres	Arithmétique – Modulo
	Introduction	Théorie	Propriétés	Formulaire
	Applications	Calculs	Carrés	Cubes
	Jeux	Sun Zi	Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7	Log Modulaire	11^10 = 32 mod 71

CONGRUENCES – Formulaire Arithmétique modulaire: recueil des formules usuelles et moins courantes concernant le calcul des congruences.
	Sommaire de cette page >>> Relation d'équivalence >>> Formules classiques >>> Formules avancées >>> Formules avec PGCD >>> Formules multi-modulo >>> Applications classiques	Débutants Opérations Glossaire Nombres

Notations et conventions

Voir Entiers / Entiers Relatifs / PGCD / PPCM / SSI

Relation d'équivalence		haut
Congruence	La relation de congruence modulo m est une relation d'équivalence entre les nombres rationnels.

Formules classiques			haut
Hypothèses	Ces hypothèses impliquent les relations suivantes:	Exemples 1 ≡ 8 [7] et 3 ≡ 10 [7] Avec k = 2.
Translation		1 + 2 ≡ 8 + 2 ≡ 3 [7] 1 – 2 ≡ 8 – 2 ≡ –1 ≡ 6 [7] (Rappel: –1 + 7 = 6)
Changement d'échelle		1 x 2 ≡ 8 x 2 ≡ 2 [7] 1 x 2 ≡ 8 x 2 ≡ 2 [14]
Addition mutuelle		1 + 3 ≡ 8 + 10 ≡ 4 [7] 1 – 3 ≡ 8 – 10 ≡ –2 ≡ 5 [7]
Multiplication mutuelle		1 x 3 ≡ 8 x 10 ≡ 3 [7] (80 = 11 x 7 + 3)
Puissance (k > 0)		1^3 ≡ 8^3 ≡ 1 [7] (8^3 = 512 = 73 x 7 + 1)
		Faux en général
Attention		Aucune conclusion sur a ou b (a n'est pas nul mod m, ni b)

Formules avancées				haut
Rubrique	Proposition	Implication	Exemples
Addition			1 + 3 ≡ 9 ≡ 4 [5]
			1 ≡ 9 – 3 ≡ 1 [5]
			Faux en général
Constante	et (k, m) = 1		4 x 7 ≡ 9 x 7 ≡ 3 [5] 7 et 5 sont copremiers 4 ≡ 9 [5]
	et k > 0		3 ≡ 10 [7] k = 2 6 ≡ 20 [7] 6 ≡ 20 [14]
	et (k, m) = 1		Autre formulation de la propriété précédente.

Division	et d est un diviseur de m		1 ≡ 15 ≡ 29 [14] 1 ≡ 15 ≡ 29 [7]
	et (d, m) = 1		6 ≡ 34 [7] d = 2 3 ≡ 17 [7]
	et d est un diviseur commun de a et b, premier avec m		3 ≡ 63 [5] d = 3 1 ≡ 21 [5]
	et d est un diviseur commun de a, b et m		10 ≡ 25 [15] d = 5 2 ≡ 5 [3]

Puissance			Faux en général
	et (a, m) = 1		phi(5) = 4 2 ≡ 6 [4] 3 ≡ 8 [5] 2^3 ≡ 6^8 [5]

Fonction

f(x) polynôme à coefficients entiers

f(x) = 2x + 3 3 ≡ 14 [11] 9 ≡ 31 [11]

Formules avec PGCD				haut
Rubrique	Proposition	Implication	Exemples
Inverse		SSI (a, m) = 1	Inverses de 3 mod 5 [2, 7, 12, …, 2 + 5k]
	Si (a, m) = 1, tel que		(7, 11) = 1 7 x 8 = 56 ≡ 1 [11]
	Si a^-1 existe		3 ≡ 13 [5] 3 x 2 = 6 ≡ 1 [5] 13 x 2 = 26 ≡ 1 [5] 13 x 7 = 91 ≡ 1 [5]
	et (a, m) = 1		4x = 3 [7] Inverse de 4 = 2 [7] x = 2 x 3 = 6 et: 4 x 6 = 24 ≡ 3 [7]
	(a, m) = 1		4 x 9 = 36 ≡ 1 [7] 4 x 16 = 61 ≡ 1 [7] 9 ≡ 16 ≡ 2 [7]
Fraction (exemple)

Égalités			/
		SSI m|a	14 ≡ 0 [7] et 14 = 2x7
		(a, m) = (b, m)	Appartenance à la même classe; même PGCD
			4x1 ≡ 4 x 6 ≡ 4 [10] (4, 10= ) 2 1 ≡ 6 ≡ [10/2 = 5]

Formules multi-modulo				haut
Rubrique	Proposition	Implication	Exemples
Deux	et m multiple de m'		3 ≡ 13 [10] 3 ≡ 13 [5]
	(m, m') = 1		(4, 5) = 1 3 ≡ 23 [4] 3 ≡ 23 [5] 3 ≡ 23 [20]
			[12, 18] = 36 3 ≡ 39 [12] 3 ≡ 39 [18] 3 ≡ 39 [36]
Multiple	m multiple de m1, m2, m3, …	…	3 ≡ 103 [100] 3 ≡ 103 [50] 3 ≡ 103 [25] 3 ≡ 103 [20] 3 ≡ 103 [10] 3 ≡ 103 [5]
	pour i = {1, 2, …, r}		[4, 6, 8] = 24 3 ≡ 27 [4] 3 ≡ 27 [6] 3 ≡ 27 [8] 3 ≡ 27 [24]

Merci à Dragos Zaharia pour ses remarques

Applications classiques			haut
Petit théorème de Fermat	Si p est premier et ne divise pas a, alors:
Théorème de Wilson	Le nombre p est premier SSI
Théorème des restes chinois	Pour tous (a, b) et (m, n) – m et n premiers entre eux – il existe un nombre unique x tel que: mn^-1 est l'inverse de m modulo n.
Théorème d'Euler	Si a et n sont premiers entre eux: (Phi est la fonction totient)
Théorème de Lagrange	Soit un polynôme à coefficients entiers et a0 non nul mod p	possède au plus n racines.
Résidu quadratique	Trouver x sachant que p et q sont des nombres premiers impairs distincts

Haut de page

Suite Retour	Congruences propriétés Congruences – Exemples de calculs Approche
Voir	Carrés Divisibilité Clé de divisibilité, une application de la théorie du modulo La division Exemple d'application du modulo en Codage RSA
Aussi	Calcul mental Géométrie Nombres Premiers Nombres Rationnels Preuve par 9 – Glossaire Théorie des nombres Variations sur les carrés
Livre	Algèbre 1 – Cours et 600 exercices corrigés – 1^re année MPSI, PCSI, PTSI – Jean-Marie Monier – Dunod – 1996
Site	Congruences dans Z - Spé Maths – J'ai compris.com – Vidéo avec exercices corrigés Chapitre 3 : congruences et arithmétique modulaire Congruence sur les entiers - Wikipédia Congruence – Wolfram MathWorld Lecture 3: Congruences Lecture on Number Theory – Lars Ake Lindahl – 2002 – pdf 95 pages
Cette page	http://villemin.gerard.free.fr/ThNbDemo/ModFormu.htm