différence des carrés - propriété : calcul des valeurs de départ

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/12/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Partitions
Débutants Addition	Variations sur les carrés				Glossaire Addition
INDEX PARTITION	Carrés	Chiffres répétés	Repdigits
	Produits	66 x 67 …	66 x 99 …	Factorisation
	Sommes	Somme double
	Différences	Propriétés	Écart 1, 2, …	Trouver la dif. des carrés
		Table 1 à 100	Repdigits	Table des Repdigits
		Curiosités	Tableau synthèse	a² – b² = c² – d²
	Sommaire de cette page >>> Faisabilité et calculs >>> Nombres de 0 à 30 >>> Records >>> Cas d'un nombre unique >>> Méthode pratique		>>> Exemple avec 100 >>> Exemple avec 60 >>> Impossibilité >>> Bilan >>> Chaines de triplets de Pythagore

DIFFÉRENCE des carrés

de deux nombres

On donne N. L'exprimer sous la forme d'une différence de deux carrés.

Pas toujours possible!

N = n² – m² Valeurs de n et m ?

Construction de chaines infinies de triplets de Pythagore.

Nombres doublement pairs (divisibles par 4)

Théorème

Tous les multiples de 4 (sauf 4) sont, au moins une fois, différence de deux carrés. Les autres nombres pairs ne sont jamais différence de deux carrés.

Il suffit de considérer un des produits de deux nombres pairs (a٠b) et d'appliquer une identité remarquable:
(a – b) (a + b) = a² – b²

Exemple

Record de présentations

Voir Table / Brève 56-1110

FAISABILITÉ ET CALCULS

Rappel

Deux nombres	n et m
leur somme	s = n + m
Leur différence	e = n – m
La différence de leur carré
N = n² – m²	= (n + m) (n – m)
N= n² – m²	= s . e

Selon la valeur de e

e = 1 => s = N

N est la différence des carrés de

deux nombres consécutifs

dont la somme est N.

3² – 2² = 5

Notez que, de ce fait, n² – m² = 1 est impossible (sauf 1² – 0²)

De même avec 2: si e = 1 la somme est égale à 2 ; impossible.

Et, si e = 2 la somme vaut 1: impossible

e > 1 => N est un nombre composé

N ne peut s'exprimer sous la forme

d'une différence de carrés de

deux nombres non consécutifs

que s'il est composé.

Voir conclusions plus précises en Bilan

Calcul

N =	= (n + m) (n – m)
N =	= s . e
n + m	= s
n – m	= e
2n	= s + e
n	= (s + e) / 2
m	= (s – e) / 2

Nombres de 0 à 30

De 0 à 10 toutes les possibilités s.e

En jaune pale les nombres différences de carrés, en jaune foncé, double possibilité.

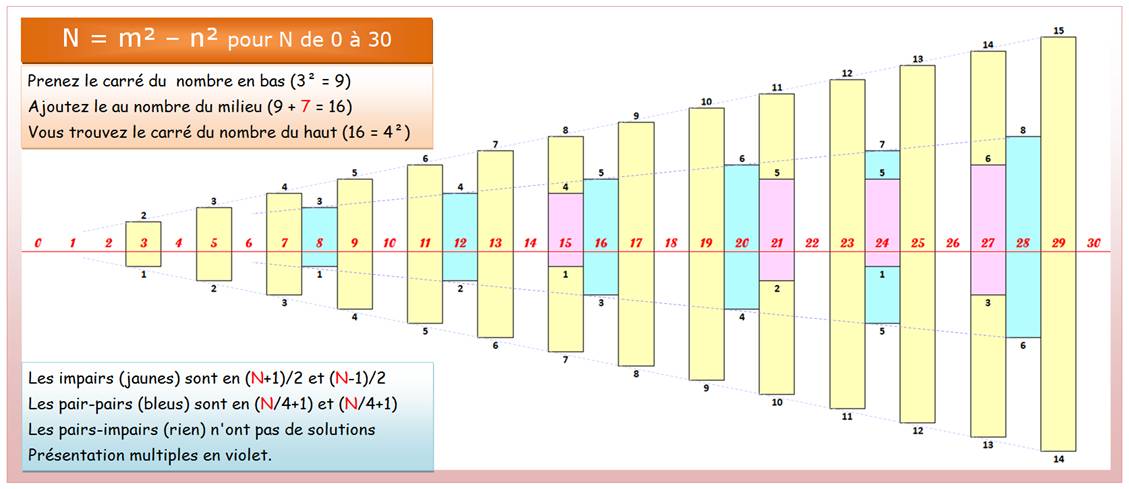
Illustration: structure des différences de carrés donnant les nombres successifs

Record de quantité de présentations

Liste: 3, 15, 45, 96, 192, 240, 480, 720, 960, 1440, 2880, 3360, 5040, 6720, 10080, 20160, 30240, 40320, 60480, 80640, 100800, 110880, 181440, 201600, 221760, 332640, 443520, 665280, 887040, …

Détails

Voir Tables / Brève 562

Cas d'un nombre unique

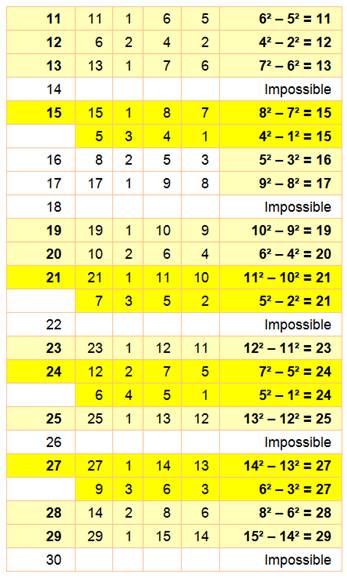
Toutes les différences jusqu'à n = 50

Exemple de lecture: 48 = 4³ – 4² = 2⁶ – 2⁴

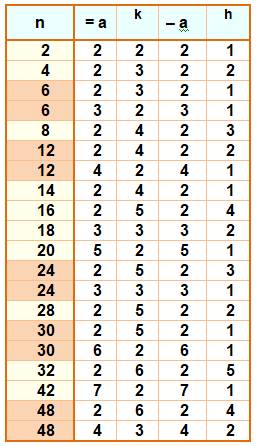
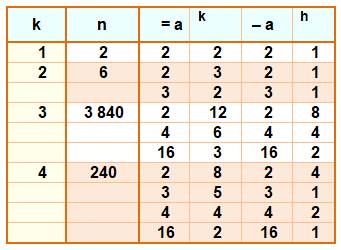
Record de quantité de différences pour un même nombre

Aucun k = 5 jusqu'à n = 10 000, a = k = h = 100.

Voir Table complète / Table des différences de puissances à écart minimum

Dans le DicoNombre voir: Nombre 6 / Nombre 240 / Nombre 3 840

MÉTHODE PRATIQUE

Procédé

Soit un nombre	N	100
Un diviseur	e	2
Le quotient	s = N / e	50
Premier nombre Ce nombre doit être entier	n = (s + e) / 2	52/2 = 26
Deuxième nombre	m = (s – e) / 2	48/2 = 24
Différence de carrés	N = n² – m²	100 = 26² - 24²

Autre exemple

Soit un nombre	N	100
Un diviseur	e	5
Le quotient	s = N / e	20
Premier nombre Ce nombre doit être entier s + e doit être pair	n = (s + e) / 2	25/2 = *12,5*
Cette décomposition n'est pas réalisable

EXEMPLE AVEC 100

Recherche des diviseurs et sommes paires

					*Somme*	*Paire*
*Diviseurs de 100*	2	2	5	5
100 = Produit de deux nombres 5 Possibilités:	1		100		101	NON
	2		50		52	OUI
	4		25		29	NON
	5		20		25	NON
	10		10		20	OUI

L'un des nombres est la moitié* de la somme*	52 / 2 = 26
L'autre est cette moitié moins* le plus petit diviseur*	26 - 2 = 24

Deux seules décomposition de 100

en différences de carrés

100 = 26² - 24²

100 = 10² - 0²

EXEMPLE AVEC 60

Recherche des diviseurs et sommes paires

					*Somme*	*Paire*
*Diviseurs de 60*	2	2	3	5
60 = Produit de deux nombres 6 Possibilités:	1		60		61
	2		30		32	OUI
	3		20		23
	4		15		19
	5		12		17
	6		10		16	OUI

Deux seules décomposition de 60

en différences de carrés

60 = 16² - 14²

60 = 8² - 2²

IMPOSSIBILITÉ

Voyons les cas où la mise sous forme de différences de carrés est impossible

On a vu que	n = (s + e) / 2	doit être entier
Ou divisible par 2 , soit	(s + e)	pair
Obtenu si	s et e	sont pairs
ou si	s et e	sont impairs
Donc dans la cas où	e est pair s est impair	ça ne marche pas
Le plus simple	e = 2 et s = 2k+1	ça suffit
N	= 2 (2k + 1)	¹ m² - n²

Les nombres en

2 (2k + 1)

ne peuvent être exprimés sous la forme

d'une différence de deux carrés.

Les nombres en 2 (2k + 1)

Ce sont les nombres pairs qui divisé par 2 donnent un nombre impair (dits pairs-impairs).

Ce sont les nombres en progression arithmétique de raison 4 à partir de 2.

2, 6, 10, 14, 18, 22, 26 …

Voir la table des nombres de 1 à 100

et leurs expressions en différences de carrés

BILAN

Tous les nombres peuvent être décomposés en différences de carrés

N = n² – m² = e . s

avec e = n – m et s = n + m

Sauf ceux de la forme

2 (2k + 1)

Ceux qui sont impairs donnent, en particulier deux nombres consécutifs:

N = { (N + 1) / 2 }² – { (N – 1) / 2 }²

Chaines de triplets de Pythagore
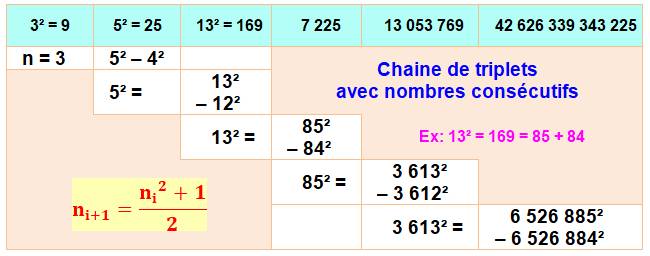
Prenons le nombre 3 et son carré On continue avec 5 et son carré Il est possible de poursuivre sans fin	9 = 5 + 4 = 5² – 4² 25 = 13 + 12 = 13² – 12² 169 = 85 + 4 = 85² – 84²
Il est possible de constituer une chaine infinie pour tout nombre impair. Les premiers nombres pour les premières chaines [3, 5, 13, 85, 3613, 6526885] [5, 13, 85, 3613, 6526885, 21300113901613] [7, 25, 313, 48985, 1199765113, 719718163185951385] [9, 41, 841, 353641, 62530978441, 1955061632394403395241] [11, 61, 1861, 1731661, 1499324909461, 1123987592065117923655261] [13, 85, 3613, 6526885, 21300113901613, 226847426110843688722000885] [15, 113, 6385, 20384113, 207756031398385, 21581284291203366989290304113] Ex: 113² – 112² = 15² Même liste mais avec les carrés [3, 25, 169, 7225, 13053769, 42600227803225] [5, 169, 7225, 13053769, 42600227803225, 453694852221687377444001769] [7, 625, 97969, 2399530225, 1439436326371902769, 517994234419759747473589427583418225] [9, 1681, 707281, 125061956881, 3910123264788806790481, 3822265986460669315287975024801628461448081] [11, 3721, 3463321, 2998649818921, 2247975184130235847310521, 1263348107116341940414873643024196400115172978121] [13, 7225, 13053769, 42600227803225, 453694852221687377444001769, 51459754733114686962148583993443846186613037940783225] [15, 12769, 40768225, 415512062796769, 43162568582406733978580608225, 465751831657741214303598968917332180433794527992024716769]

Suite	Table des différences de carrés de 1 à 100 S'y retrouver
Voir	Addition – Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach Identités remarquables Impairs Machine des frères Carissan Nombres consécutifs Nombres consécutifs Palindromes Repdigit Répétition de motifs TABLES – Index
DicoNombre	Nombre 60 Nombre 111 Nombre 100
Cette page	http://villemin.gerard.free.fr/Wwwgvmm\Addition\P100a500\Difcartr.htm