Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 20/12/2022 M'écrire Brèves de Maths

INDEX Triangles Types de triangles Géométrie	TRIANGLES à plusieurs
	Semblables	Isométriques	Tous les cas

Faites un double-clic pour un retour en haut de page

Triangles: semblables et isométriques Page récapitulative des cas de similitudes et d'isométries des triangles, y compris en cas de côtés parallèles ou perpendiculaires deux à deux. Tous les cas se ramènent aux trois théorèmes des triangles semblables et aux trois théorèmes d'égalité des triangles. Revue de détail …
	Sommaire de cette page >>> Égal, Isométrique, congruence >>> Trois côtés connus >>> Droites dans le cas d'isométrie >>> Deux côtés connus >>> Un côté connu >>> Semblables >>> Triangles particuliers >>> Bilan	Débutants Géométrie Glossaire Géométrie

Égal, isométrique, congruence

Autrefois, ou encore en petites classes, on disait que les triangles de cette figure sont égaux. On préfère dire qu'ils sont isométriques, c'est-à-dire qu'ils ont mêmes mesures. Les triangles marrons sont directement superposables (par glissement): ils résultent d'une translation avec, ou non, une rotation. Ils sont congruents. Ils sont obtenus par isométrie directe ou isométrie positive ou déplacement. Les triangles verts sont isométriques, mais ne sont superposables que par retournement (symétrie axiale). Ces types de triangles sont obtenus par isométrie inverse ou retournement.

Voir Toutes les transformations / Isométrique dans le dico

Trois côtés connus		haut
Construction Un côté AB de longueur c. Cercle (A, b) Ce qui signifie de centre A et de rayon b). Cercle (B, a). Intersection C, troisième sommet du triangle Propriétés Le triangle est entièrement déterminé par la longueur de ses trois côtés.
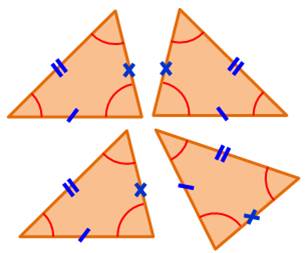
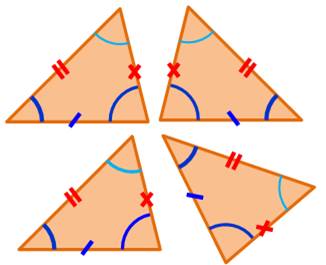
Premier cas d'égalité des triangles Si deux triangles ont trois côtés respectivement égaux, ils sont isométriques. Condition nécessaire et suffisante. La valeur de chaque angle est imposée. Les triangles sont semblables, a fortiori.

Droites dans le cas d'isométrie		haut
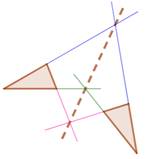
Droites sur les côtés Dans le cas de deux triangles superposables par glissement (congruents), les droites prolongeant les côtés se coupent selon le même angle. La réciproque n'est pas vraie: trois couples de droites qui se coupent selon le même angle ne forment forcément deux triangles isométriques. Dans le cas d'une symétrie axiale (triangles superposable par retournement), les côtés se coupent deux à deux sur l'axe de symétrie. Réciproquement: trois couples de droites symétriques qui se coupent sur l'axe de symétrie, forment deux triangles isométriques.	Glissement Symétrie axiale
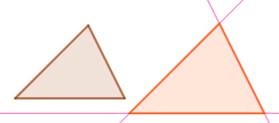
Droites parallèles aux côtés Des droites parallèles aux côtés forment un triangle semblable. Réciproquement: trois couples de droites parallèles deux à deux forment des triangles semblables. Droites perpendiculaires* aux côtés Des droites perpendiculaires aux côtés forment un des triangles semblables. Réciproquement: trois couples de droites perpendiculaires deux à deux forment des triangles semblables. * On dit perpendiculaires car on est dans le plan; orthogonale englobe tous les cas, même dans l'espace où les droites de ne rencontrent pas.
Cas du triangle rectangle Est-ce que la présence d'un angle droit modifie les choses ? Pas vraiment ? Si les deux triangles ont tous leurs côtés respectivement perpendiculaires (vert) ou deux perpendiculaires et un parallèle (violet), ils sont semblables. La seule connaissance d'un élément supplémentaire (longueur ou angle) les rend isométriques.

Deux côtés connus		haut
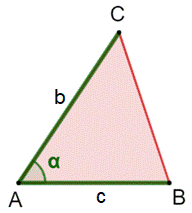
UN ANGLE INTÉRIEUR aux deux côtés connus Construction Un segment AB de longueur c. Un angle de valeur alpha à partir de A. Report de la longueur b sur le côté AC de l'angle. Propriétés Le triangle est parfaitement déterminé avec ces trois paramètres (a, b, alpha).	2C + 1Ai = 1T (deux Côtés + un Angle intérieur = un Triangle bien défini)
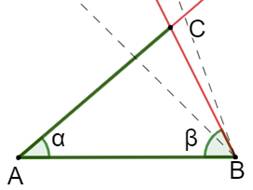
UN ANGLE EXTÉRIEUR à deux côtés connus Construction Un segment de longueur c. Angle alpha à partir d'une des extrémités du segment. Cercle de rayon a, à partir de l'autre extrémité. Propriétés Avec ces trois paramètres (a, b, alpha), il existe deux triangles possibles.	2C + 1Ae = 2T
DEUX ANGLES connus (le troisième est imposé) En général impossible, sauf pour une seule longueur du troisième côté. Voir CAS un côté et deux angles.	2C + 2A = 0T
Deuxième cas d'égalité des triangles Si deux triangles ont un angle égal compris entre deux côtés égaux, ils sont isométriques. Condition nécessaire et suffisante. La valeur de chacun des trois autres paramètres (rouges) est imposée.	Triangles avec 2C + 1Ai

Un côté connu		haut
DEUX ANGLES INTÉRIEURS Construction Un segment AB de longueur c. Deux angles de valeur alpha et béta à partir des deux extrémités Propriétés Le triangle est parfaitement déterminé avec ces trois paramètres (c, alpha et béta).	1C + 2Ai = 1T
DEUX ANGLES dont un EXTÉRIEUR Construction Un segment AB de longueur c. Un angle alpha sur une extrémité du segment. Un angle gamma à partir d'un point sur le côté de l'angle formé. Parallèle à ce nouveau côté et passant par le deuxième extrémité du segment. Plus simple Calculer béta = 180 – alpha – gamma Reprendre la construction ci-dessus. Propriétés Le triangle est parfaitement déterminé avec ces trois paramètres (c, alpha et gamma).	1C + 2Ai = 1T
UN ANGLE Avec la longueur d'un côté et la valeur d'un angle, il est impossible de définir un triangle.	1C + 1A = indéterminé
Troisième cas d'égalité des triangles Si deux triangles ont un côté égal et deux angles respectivement égaux, ils sont isométriques. Condition nécessaire et suffisante. La valeur de chacun des trois autres paramètres (rouges) est imposée.

Semblables		haut
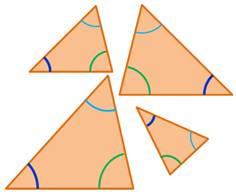
Deux triangles sont semblables si leurs angles sont respectivement égaux. Ce qui est vrai avec deux seulement (car la somme des trois vaut 180°). Les longueurs des côtés sont respectivement proportionnelles. Une longueur égale pour deux côtés correspondants, les rend isométriques.

Triangles particuliers		haut
Présentation du tableau On identifie les cas d'isométrie et de similitude des triangles équilatéraux, isocèles et rectangles. Chaque type possède des propriétés qui limitent les exigences sur les paramètres identiques. La colonne Cas, rappelle les cas d'égalités énoncés ci-dessus.

Bilan

L'analyse détaillée montre que tous les cas étudiés remontent aux trois théorèmes connus de similitudes et aux trois théorèmes connus d'isométrie (d'égalité).

Dans tous les cas, il est nécessaire de connaitre trois paramètres.

Avec les parallèles ou les perpendiculaires, on fixe implicitement un angle. Alors deux autres paramètres suffisent.

Citons les cas où tous les côtés sont parallèles ou orthogonaux deux à deux, alors les triangles sont semblables.

Ou encore, le cas de deux triangles rectangles où tous les côtés sont orthogonaux deux à deux, alors ils sont semblables et avec une donnée supplémentaire, ils sont isométriques.

Haut de page (ou double-clic)

Retour	Égalité
Suite	Transformation – Débutant Transformation – Glossaire Distance
Voir	Géométrie – Index Histoire : Euclide, Archimède … Identités algébriques Isopérimètre Jeux – Index Les Éléments Milieu d'un segment	Nombres triangle Ordre – Glossaire Points Polygones Symétries motifs de frises et tapisseries Triangles semblables
Sites
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/egaliteT.htm