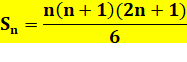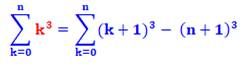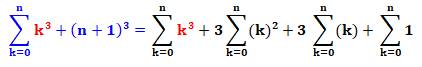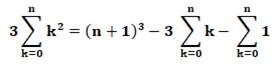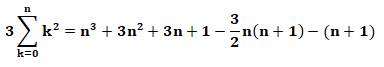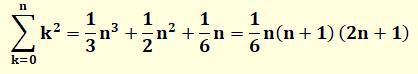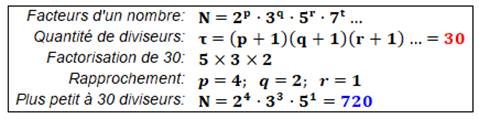Brèves de maths 20

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 20

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

380. Somme des carrés
Exemples 1² + 2² = 5 1² + 2² 3² = 14 1² + 2² 3² + 4² = 30 1² + 2² 3² + 4² + 5² = 55 Etc.		Formule Applications S₅ = 5 x 6 x 11 / 6 = 55 S₆ = 6 x 7 x 13 / 6 = 91
Brèves associées	>>> Somme des entiers		>>> Somme des inverses des carrés
Pour en savoir plus	>>> Somme des carrés		>>> Carte postale 3205

381. Calcul modulo
Prouver que 5²¹ – 7¹² est divisible par 11 sans effectuer le calcul. Petit théorème de Fermat Si p premier, et (a, p) premiers entre eux. Application		Calculs en modulo 11 Ce nombre est donc divisible par 11.
Brèves associées	>>> Petit théorème de Fermat		>>> Calcul modulo de 5⁶ – 7⁴
Pour en savoir plus	>>> Calcul modulo (Congruence)		>>> Carte postale 2305

382. Arc de cercle du jardinier
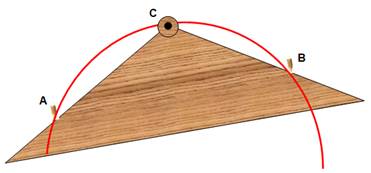
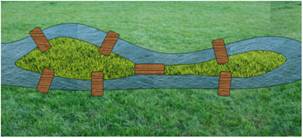
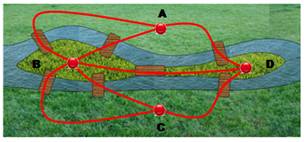
But On désire dessiner au sol l'arc ABC (cas du jardinier ou du maçon qui n'a pas accès au centre du cercle). Cet outillage permet de construire l'arc de cercle montré ici en rouge. Construction Construire un triangle solide avec un sommet en C et ses deux côtés passant par A et B. En faisant pivoter le triangle, tout en conservant le contact avec les points A et B, le crayon en C dessine l'arc de cercle.		Gabarit de traçage Principe utilisé: quel que soit le point C sur le cercle, l'angle ACB qui intercepte la corde AB (du même côté) est constant.
Brèves associées	>>> Constructions du jardinier		>>> Tangente sans le centre
Pour en savoir plus	>>> Construction du cercle sans le centre		>>> Cercle >>> Angles interceptés

383. Combien de rectangles ?
Combien de carrés dans ce quadrillage ? Dénombrement par comptage Petits carrés (taille 1): 6 x 6 = 36 Carrés (taille 2): 5 x 5 = 25 Carrés (taille 3): 4 x 4 = 16 Carrés (taille 4): 3 x 3 = 9 Carrés (taille 5): 2 x 2 = 4 Grand carré (taille 6): 1 Bilan: 1 + 4 + 9 + 16 + 25 + 36 = 6 x 7 x 13 / 6 = 91
Combien de rectangles dans ce quadrillage ? Dénombrement par comptage Carrés: 91 (cf. ci-dessus) Rectangles (1x2): 2 x 5 x 6 = 60 Rectangles (1x3): 2 x 4 x 6 = 48 Etc. Fastidieux ! Note: Pour ceux qui voudraient poursuivre le décompte par comptage: 91 + 2x6 (5+4+2+1) + 2x5 (3+4+2+1) + 2x4 (3+2+1) + 2x3 (2+1) + 2x2 = 441		Dénombrement par raisonnement Les rectangles sont formés par un couple de droites horizontales non confondues et un couple de droites verticales non confondues. Une droite horizontale parmi 7 étant choisie, il reste 6 possibilités pour la seconde. Mais, en comptant de cette manière, on doublonne. Bilan: 7 x 6 / 2 = 21 couples Même chose en vertical: 21 couples Bilan: 21 x 21 = 441 rectangles.
Brèves associées	>>> Tirage des boules
Pour en savoir plus	>>> Bases du dénombrement		>>> Somme des carrés

384. Nombres auto-descriptifs
Nombres dont les chiffres indiquent la quantité de chiffres qu'ils contiennent. Ce nombre (1210) contient : un 0, deux 1, un 2 et zéro 3.
Brèves associées	>>> Nombres de Harshad	>>> Nombres narcissiques
Pour en savoir plus	>>> Nombres auto-descriptifs	>>> La suite qui se lit

385. Nombres décimaux
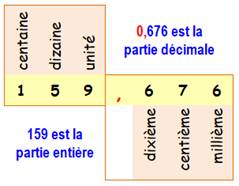
Les nombres décimaux sont des nombres à virgule dont la quantité de chiffres est limitée. Ils peuvent tous se mettre sous la forme d'une fraction avec un dénominateur en puissances de 10. Autrement dit, ce sont des nombres rationnels à développement limité. Définition			Exemples de nombres décimaux Notations
Brèves associées	>>> Nombres entiers >>> Nombres premiers	>>> Nombres géométriques
Pour en savoir plus	>>> Nombres décimaux	>>> Type de nombres

386. Valeurs trigonométriques
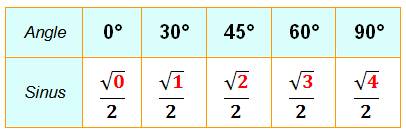
Le tableau montre un moyen simple pour mémoriser les valeurs du sinus des angles principaux. Pour le cosinus prendre l'angle complémentaire. Ainsi: cos 60° = sin 30° = 1/2
On trouve parfois ce schéma avec la main
Brèves associées	>>> Mesurer les angles
Pour en savoir plus	>>> Valeurs trigonométriques >>> Table des valeurs	>>> Trigonométrie >>> Terrain de jeu de la trigonométrie

387. Somme des carrés des entiers
La recherche de l'expression donnant la somme des carrés de 1 à n peut être réalisée en résolvant une équation. Celle-ci commence en considérant la somme des cubes. Heureusement cette somme va disparaitre dans les calculs. L'astuce initiale peut être vérifiée en prenant un exemple numérique. Le même principe permet le calcul de la somme des cubes et des puissances plus élevées.		L'astuce de départ et le calcul en découle
Brèves associées	>>> Somme de chiffres identique et divisibilité par 9 >>> Somme de produits de premiers – Divisibilité
Pour en savoir plus	>>> Somme des carrés des entiers – Démonstration détaillée

388. Nombre 3 367
Pour multiplier 3 367 par un nombre de 2 chiffres xy, il suffit de diviser xyxyxy par 3. Généralisation à tous les nombres avec x = dizaines et y = unités, mais attention aux retenues. Explication: n = 10x + y 3 367 n = 3 367 (10x + y) = 33 670x + 3 367y et: xyxyxy = 10 000(10x + y) + 100(10x + y) + 10x + y = 101 010x + 10 101y xyxyxy / 3 = 33 670x + 3 367y		Exemples
Brèves associées	>>> Multiplication rapide		>>> Addition – Truc de calcul mental
Pour en savoir plus	>>> Nombre 3 367		>>> Calcul mental – Index

389. Algèbre ou Logique de Boole
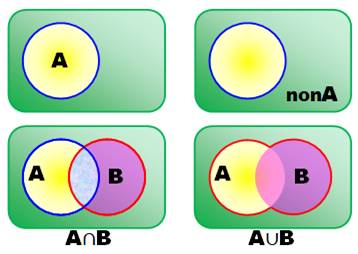
Approche algébrique de la logique. Permet de modéliser des raisonnements logiques. Créée par le britannique George Boole en 1854. Applications en informatique. La figure montre quelques exemples de représentations des fonctions logiques. Équivalence entre ces notations Conjonction Disjonction		Identité Inversion Intersection Union
Brèves associées	>>> Diagramme de Venn et dénombrement
Pour en savoir plus	>>> Logique de Boole		>>> Logique – Index >>> Vocabualire de la logique

390. Le faux billet de 50 euros
Vous payez un achat avec un billet de 50 euros que le marchand refuse au motif qu'il est faux. Vous sortez un autre billet, authentique celui-là. Double peine: vous avez été floué de 50 euros avec ce faux billet et vous devez payer 50 euros en plus; cela fait une perte de 100 euros. Vrai ?		Pas du tout ! Oubliez un instant le faux billet. Finalement, vous faites un achat de 50 euros que vous payez normalement, comme d'habitude ! Maintenant, revenez au faux billet, il vous a coûté 50 euros soit par un échange de billets ou soit par la rémunération d'un travail ou d'un objet. Comme si vous aviez eu 0 euros au lieu de 50. Ces 50 euros en faux billet sont bel et bien perdus. Soit une perte de 50 euros seulement.
Brèves associées	>>> Énigme des 30 euros		>>> Énigmes en brèves
Pour en savoir plus	>>> Énigme des 30 euros		>>> Énigmes – Index

391. Nombre RSA record
Nombre RSA Un nombre RSA est le produit de deux nombres premiers p et q très grands. Alors qu'il est facile de les multiplier, l'opération inverse, trouver p et q, connaissant N, n'est pas chose facile. De tels nombres N sont des nombres RSA.		Historique Le nombre RSA 100 (330 bits – 100 chiffres) a été factorisé en 1991 Le nombre RSA 768 (768 bits – 232 chiffres) en 2009, précédent record. Record Le nombre RSA 240 (795 bits – 240 chiffres) en 2019. Cryptage Le nombre RSA 2048 (2 048 bits – 617 chiffres) est loin d'être cassé. Des nombres de cette taille sont recommandés pour réaliser la clé de chiffrement RSA.
Brèves associées	>>> Code César		>>> Brèves de cryptologie
Pour en savoir plus	>>> Nombre RSA >>> Chiffrement RSA		>>> Multiplication de grands nombres >>> Principes de factorisation

392. IA et incomplétude
Théorème d'incomplétude de Gödel (1931) La plupart des systèmes formels peuvent formuler des énoncés corrects qui ne sont ni démontrables, ni infirmables: ils sont indécidables. Est-ce applicable à l'informatique ? Oui ! Savoir si un programme informatique va s'arrêter de calculer est une proposition indécidable. Indécidabilité ? Pas de risque pour les programmes d'IA actuels, ils sont encore trop basiques, occupés à faire des tris. Le jour où, ce niveau sommaire sera dépassé, et selon le théorème de Gödel, on butera sur le mur de l'indécidabilité.		Cas de l'apprentissage par les machines L'apprentissage machine (machine learning) actuel n'en est qu'à ses premiers pas. Il n'est pas concerné par le problème d'indécidabilité. Comment la machine apprend ? Les programmes d'apprentissage, comme les réseaux de neurones artificiels fonctionnent sur le principe de l'apprentissage statistique par l'exemple. Pour reconnaître un animal, on entraîne l'algorithme avec des millions d'images de l'animal à reconnaitre. Le réseaux de neurones enregistre l'image qu'il s'en fait et la modifie avec les nuances apportées à chaque expérience. À la longue, le programme reconnait l'objet avec un taux d'erreur acceptable et contrôlable.
Brèves associées	>>> Algorithmes		>>> Intelligence artificielle (IA)
Pour en savoir plus	>>> Intelligence artificielle >>> Réseaux de neurones		>>> Théorème d'incomplétude >>> Paradoxes

393. Sept ponts de Königsberg
Pendant son séjour à l'Académie des sciences de Saint-Pétersbourg, Euler reçut une lettre qui provenait de la ville pittoresque de Königsberg en Prusse (Kaliningrad dans la Russie actuelle). Morcelée par les bras de la rivière Pregel, la ville consistait en quatre quartiers séparés, reliés par sept ponts. Le maire de la ville voulait organiser un circuit à pied de Königsberg de telle manière que les touristes franchissent tous les ponts. Euler montre qu'il est tout bonnement impossible de parcourir Königsberg à pied de la manière souhaitée et il explique: le graphe équivalent ne doit comporter que des nœuds pairs (quantité paire de branches partant d'un nœud). La théorie des graphes était née.		La topologie de la ville avec sept ponts Graphe des chemins possibles
Brèves associées	>>> Chemin eulérien des nombres
Pour en savoir plus	>>> Ponts de Königsberg – Graphes eulériens		>>> Graphes planaires >>> Graphes et quatre couleurs

394. Nombres sandwiches
Nombres dont les chiffres présentent une répartition particulière: un seul nombre entre deux 1; deux nombres entre deux 2; trois nombres entre deux 3; etc. Quelles sont toutes les possibilités ? Pour 123, il y a deux solutions, l'une retournée de l'autre; Pour 1234, deux solutions; Pour 12345 et 123456, impossible; Pour 1234567, il y a 2 x 26 solutions; et avec le 8, il y en a 2 x 150		Exemples 231 213 et 312 132 (son retourné) 23 421 314 et 41 312 432 14 167 345 236 275
Brèves associées	>>> Nombres géométriques		>>> Nombres quadrillages
Pour en savoir plus	>>> Nombres sandwiches		>>> Nombres à motif – Index

395. Carrés dans le carré
Problème d'empilement optimal dans le plan qui consiste à arranger N carrés identiques dans un carré, le plus petit possible. Si n est un nombre carré, alors l'empilement est évident. Démontrer que l'empilement des carrés est optimum (aire minimale du grand carré) n'est pas simple. Elle n'est connue que pour quelques cas particuliers: 2, 3, 5, 7, 8, 14, 15, 24 et 35.		Exemple optimum pour n = 5 et n = 10
Brèves associées	>>> Carré et deux triangles équilatéraux		>>> Hexagone et triangles
Pour en savoir plus	>>> Carré dans le carré		>>> Empilement des sphères

396. Nombres friables
Un nombre dont tous les facteurs premiers sont inférieurs ou égaux à 5 sont des nombres 5-friables. Les nombres 2-friables sont les puissances de 2. Notion utile en cryptographie.		Nombres réguliers ou 5-friables 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 64, 72, 75, 80, 81, 90, 96, 100, …
Brèves associées	>>> Nombres parfaits		>>> Nombres pseudo-premiers
Pour en savoir plus	>>> Nombres friables		>>> Facteurs et diviseurs

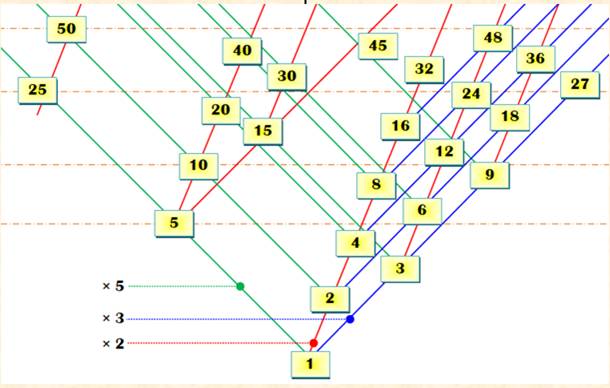
397. Diagramme de Hasse
Façon élégante de représenter tous les multiples de 2, 3 et 5. Ici jusqu'à 50
Brèves associées	>>> Nombres friables	>>> Diagramme de Venn et dénombrement
Pour en savoir plus	>>> Diagramme de Hasse	>>> Diagramme de Karnaugh

398. Suite de Kolakoski
Principe de construction Il s'agit d'une suite de 1 et de 2 qui s'auto-génère. Chaque nombre indique ce que contient la suite. Le 2 en bleu-foncé exige deux nouveaux chiffres qui seront des "2", pour assurer l'alternance. Comment poursuivre cette suite ? Le "1" qui suit le "2" bleu-foncé indique qu'il faut ajouter un seul nombre, et ce sera un "1" pour assurer l'alternance. Les 60 premiers chiffres de la suite 1221121221 2211211221 2112122112 1121221221 1212212112 1122122112 …		Exemple de construction Je lis: le 1 => il y a un chiffre, le 1; le 2 => il y a deux chiffres, le 2 par alternance; le 2 => il y a ensuite deux chiffres, le 1; etc. Suite Le 1 derrière le 2 bleu exige un chiffre et ce sera un "1". Propriétés La quantité de "1 " est égale à celle des "2", mais ce n'est pas prouvé. La suite présente une structure fractale. En transposant la suite en un nombre binaire, puis en décimal, on obtient la constante de Kolakoski: 0,79450…
Brèves associées	>>> La suite qui se lit		>>> Suite de Fibonacci
Pour en savoir plus	>>> Suite de Kolakoski		>>> Suites en général

399. Quantité de diviseurs
On se propose de trouver le plus petit nombre ayant trente diviseurs. Noter la formule qui donne cette quantité de diviseurs en fonction de la factorisation première du nombre: produit des exposants plus 1.		Démonstration Les 30 diviseurs de 720: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360, 720. Somme: 2 418. Le nombre 720 est abondant.
Brèves associées	>>> Diviseurs d'un nombre		>>> Recherche de facteurs
Pour en savoir plus	>>> Nombre 30 >>> Nombre 720		>>> Factorisation >>> Quantité de diviseurs

Anglais: What is the smallest integer which has 30 factors ? Answer: 720.

Retour	Brèves de maths – Page 19
Suite	Brèves de maths – Page 21
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve20.htm

380. Somme des carrés

381. Calcul modulo

382. Arc de cercle du jardinier

383. Combien de rectangles ?

384. Nombres auto-descriptifs

385. Nombres décimaux

386. Valeurs trigonométriques

387. Somme des carrés des entiers

388. Nombre 3 367

389. Algèbre ou Logique de Boole

390. Le faux billet de 50 euros

391. Nombre RSA record

392. IA et incomplétude

393. Sept ponts de Königsberg

394. Nombres sandwiches

395. Carrés dans le carré

396. Nombres friables

397. Diagramme de Hasse

398. Suite de Kolakoski

399. Quantité de diviseurs