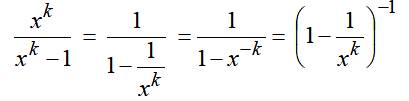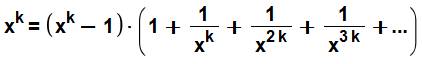|
|||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Fraction
xk / (xk – 1) Que vaut un nombre à une certaine puissance divisé par
lui-même diminué de un ? Utile dans la démonstration
de l'identité d'Euler |
|
|
||
|
Diverses formulations Ces expressions sont équivalentes Nous allons chercher une autre manière de les
exprimer en utilisant un développement en série. |
|
|
|
|
||
|
Développement en série Nous allons effectuer la division. Bilan Série des inverses du nombre aux puissances
multiples de k. Puissance en progression géométrique de
raison k |
Résultat
|
|
|
|
||||||||||||||||||||||
|
Calcul pour x = 2 et k = 2 Voici les dix premières itérations de la
série: |
5 / 4 1,
250000000 21
/ 16 1,
312500000 85
/ 64 1,
328125000 341
/ 256 1,
332031250 1365
/ 1024 1,
333007812 5461
/ 4096 1,
333251953 21845
/ 16384 1,
333312988 87381
/ 65536 1,
333328247 349525
/ 262144 1,
333332062 1398101
/ 1048576 1,
333333015 |
|||||||||||||||||||||
|
Valeur selon x et k
|
||||||||||||||||||||||
Voir Démonstration
de l'identité d'Euler
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()