Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/01/2024 M'écrire Brèves de Maths

INDEX Polygones Carrés Géométrie Dénombrement Jeux et énigmes	QUADRILATÈRES – Compter
	Quadrilatère	Triangles dans rectangle	Grille & segments
	Carré	Triangle dans le carré	Grille & triangles rectangles
	Rectangle	Carrés et cercles	Grille & triangles équilatéraux
	Trapèze	Carré (un) dans le carré	Grille & carrés
	Parallélogramme	CARRÉS dans le carré
	Losange	Carrés dans rectangle
	Polygones	Rectangles dans carré	Rectangles – Énigmes
		Rectangle dans rectangle	Pièce de puzzle
		Quadrilatère dans le carré

Faites un double-clic pour un retour en haut de page

Rectangles dans un carré Propriétés de quatre rectangles de même aire comme pavage d'un carré. Surprise ! Création d'un carré central.
	Sommaire de cette page >>> Pour se lancer … >>> Approche >>> Taille des rectangles >>> Possible ou impossibles ?	Débutants Géométrie Glossaire Géométrie

Pour se lancer …
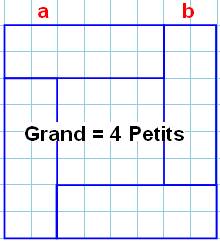
Problème Un carré. Quatre rectangles de côtés a et b disposés comme sur cette figure. Sachant que l'aire du carré extérieur est quatre fois plus grande que celle du carré intérieur, calculer la proportion entre a et b ? Calculs

Approche
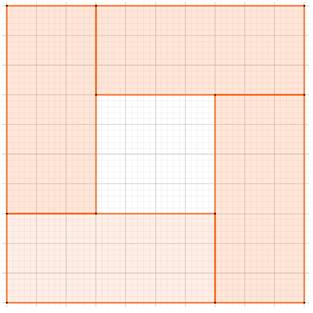
Problème Un carré; quatre rectangles de côtés a et b et d'aire identique A = ab disposés comme indiqué sur la figure. Montrer que le rectangle central est toujours un carré. Exemple Cette figure montre quatre rectangles identiques a = 7 et b = 3. Alors l'aire vaut 21 et rempli de carré d'aire 100 avec une surface d'aire 4 x 21 = 84. Le rectangle central a une aire de 100 – 84 = 16 = 4².

Taille des rectangles
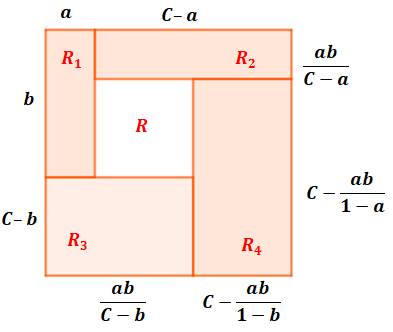
Notations Le grand carré initial à pour côté C. Prenons l'un des carrés comme référence R1 de côté a et b. Les autres dimensions s'en déduisent en cascade. Par exemple R2 longueur: C – a largeur: aire ab divisée par la longueur.

Possible ou impossibles ?
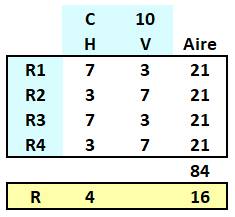
Exemple a + b = C H et V représentent les dimensions horizontale et verticale des rectangles. Avec a = 7 et b = 3 (soit a + b = 10 = C), les quatre rectangles sont identiques et l'aire vacante au centre est égale à 16, soit un carré de 4 de côté. Compte-tenu des symétries, c'est bien un carré.
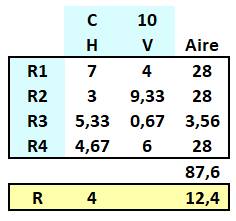
Exemple a + b > C Avec a + b supérieur au côté du carré, l'enchainent des dimensions conduit trois aires identiques mais la quatrième n'est pas satisfaire. PAS POSSIBLE !
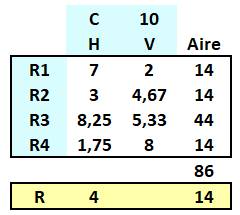
Exemple a + b < C Avec a + b inférieur au côté du carré, ce n'est pas correct non plus. PAS POSSIBLE !
Conclusion Un raisonnement conduit sur ces inégalités démontre que la seule possibilité est que a + b = C avec quatre rectangles identiques.	Avec quatre rectangles de même aire disposés dans le carré, la zone centrale est un carré.

Anglais

A square is divided into five rectangles as shown below. The four outer rectangles R₁, R₂, R₃, R₄ all have the same area. Prove that the inner rectangle R₀ is a square.

Voir Anglais pour le bac et pour les affaires

Suite	Quantité de carrés dans le quadrillage d'un rectangle Constructions élémentaires: rectangle Le terrain de basket Losange Pavage avec des rectangles Quadrilatères – Juniors Rectangle - Coordonnées intersection Rectangle d'or Rectangle et colinéarité Rectangle de Ailles Rectangles dans le cube Rectangles emboîtés
Voir	Allumettes Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie Jeux – Index
Site	Solving mathematical problems – A personal perspective – Terence Tao – Problem 4.5 page 62 – Avec la démonstration
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/RectCarr.htm