|
Édition du: 27/11/2022 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
|
|
|||
Faites un double-clic pour un retour en haut de page
![]()
|
CARRÉS entiers dans GRILLE Les carrés entiers sur une grille ont pour côtés
la suite des nombres sommes de deux carrés. Tous les nombres ne sont pas au
rendez-vous ! |
||
|
|
Sommaire de cette page >>> Les carrés dans une grille >>> Carrés constructibles >>> Diagonale et
quantité de carrés |
Débutants Glossaire |
Triangles équilatéraux
et triangles rectangles
|
Il est impossible de dessiner un triangle équilatéral
comme un hexagone sur les sommets d'une grille >>> Dénombrement des triangles rectangles sur une grille finie
>>> |
|
Nombres entiers Il s'agit d'identifier les carrés
dont les sommets sont des points de la grille. Dit-autrement: sommets dont les coordonnées sont
des nombres
entiers. Deux cas Le côté du carré est alors un nombre entier; il
est aligné sur le quadrillage. Le carré existe aussi en position inclinée et la
longueur de son côté est une racine
carrée. Côté Le théorème
de Pythagore permet le calcul de cette longueur. Avec a pas en
horizontal et b en vertical, la longueur
du côté sera: c² = a² + b² L'aire de ce carré est c². |
Carrés dessinés sur une grille
régulière
|
|
|
Question Quels sont les aires possibles parmi tous les
carrés constructibles sur une grille infinie ? Réponse Ce sont tous les nombres carrés et tous les
nombres sommes
de deux carrés. Somme de carrés Or, si tous les nombres sont sommes de quatre
carrés, ils ne sont pas tous somme de deux carrés. Selon le théorème
de Fermat, ce sont ceux dont les facteurs impairs sont égaux à 3 modulo 4
(divisés par 4, le reste est 3) Quantité De 1 à 500 seuls 178 nombres sont somme de un ou
deux carrés (35 %). |
Liste des nombres carrés et des
nombres sommes de deux carrés 0, 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25,
26, 29, 32, 34, 36, 37, 40, 41, 45, 49, 50, 52, 53, 58, 61, 64, 65, 68, 72,
73, 74, 80, 81, 82, 85, 89, 90, 97, 98, 100, 101, 104, 106, 109, 113, 116,
117, 121, 122, 125, 128, 130, 136, 137, 144, 145, 146, 148, 149, 153, 157,
160, 162, 164, 169, 170, 173, 178, 180, 181, 185, 193, 194, 196, 197, 200,
202, 205, 208, 212, 218, 221, 225, 226, 229, 232, 233, 234, 241, 242, 244,
245, 250, 256, 257, 260, 261, 265, 269, 272, 274, 277, 281, 288, 289, 290,
292, 293, 296, 298, 305, 306, 313, 314, 317, 320, 324, 325, 328, 333, 337,
338, 340, 346, 349, 353, 356, 360, 361, 362, 365, 369, 370, 373, 377, 386,
388, 389, 392, 394, 397, 400, 401, 404, 405, 409, 410, 416, 421, 424, 425,
433, 436, 441, 442, 445, 449, 450, 452, 457, 458, 461, 464, 466, 468, 477,
481, 482, 484, 485, 488, 490, 493, 500, … |
|
|
Propriété Du théorème des quatre carrés, on en déduit que
tout nombre est somme de deux nombres de cette liste. Dans la majorité des cas, de nombreuses fois. |
100 = 2 + 98 10 + 90 18 + 82 20 + 80 26 + 74 32 + 68 36 + 64 50 + 50 |
|
|
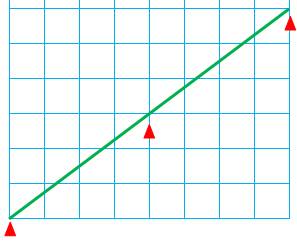
Question Sur cette grille rectangulaire 8 × 6, combien
peut-on dessiner de carrés ? Autrement-dit: par combien de points de la grille
passe cette diagonale ? Exemple Ici, on compte trois points y compris les
extrémités. Soit la possibilité de dessiner trois carrés ayant des sommets
sur la grille. L'aire est: 8² + 6² = 64 + 36 = 100 = 10² Note: entre deux flèches rouges, on reconnait le
célèbre triangle rectangle (3,
4, 5). |
La diagonale du rectangle rencontre trois points de la grille
|
|
|
Explication La diagonale progresse de 6 carreaux en y pour 8 en x soit la fraction 6/8 qui se réduit
en 3/4 (fraction irréductible). Ce qui veut dire que la diagonale rejoint un
point du quadrillage chaque fois que x progresse de 4. La quantité de points rencontrés sur la
grille est alors: Q = 1 + 8/4 = 3 |
Méthode Avec un rectangle (m, n). Réduire au maximum la fraction n/m en a/b. (a et b sont premiers entre
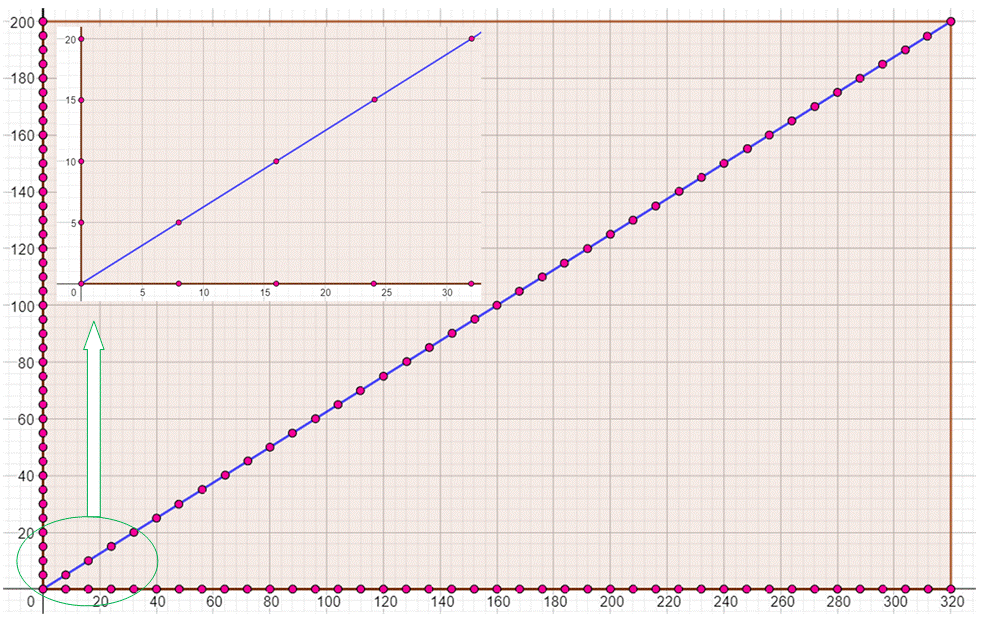
eux). La quantité de points sur la diagonale est: Q = m / b Exemple (Illustration
ci-dessous) m = 320 et
n = 200 Fraction 200/320 = 5/8 On aurait pu prendre 200/5 = 40 Q = 1 + 320/8 = 41. |
|
Exemple: rectangle 320 × 200
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |