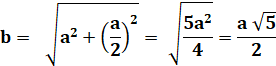|
Édition du: 19/02/2025 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
TRIANGLE inscrit dans le CARRÉ ou
dans le rectangle
Construction du triangle isocèle et du triangle
équilatéral dans un carré. |
||
|
|
Sommaire de cette page >>> L'angle du triangle
inscrit dans le carré >>> Triangle isocèle dans
le carré >>> Triangle
équilatéral dans le carré |
Débutants Glossaire |
|
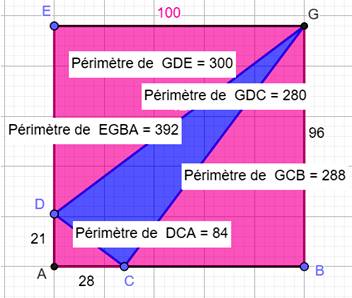
Un
rectangle ABCD (100 x 96). Ayant
choisi les points D et C, on trouve les périmètres des trois triangles
rectangles périphériques: 300, 288 et 84. Quel
est le périmètre du triangle bleu ? |
|
Un problème posé en quatrième. Il semble simple, mais sans doute
impossible sans l'aide d'une construction astucieuse. Démarche pour trouver
cette construction. |
||
|
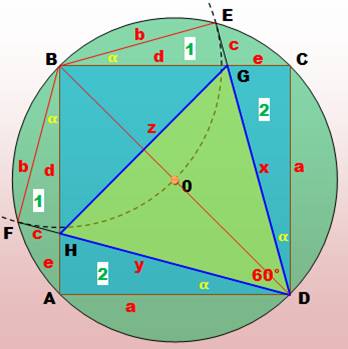
Construction Un
carré et un triangle inscrit dans ce carré. Avec les deux angles indiqués,
trouver la valeur de l'angle alpha. Pistes Avec
les angles donnés et du fait que la somme des angles d'un triangle égal à 180°,
on en déduit les angles indiqués sur la deuxième figure. Cependant
les angles α, α', β et β' restent inconnus. On
sait que:
Merveilleux!
Quatre équations pour quatre inconnues. Hélas, l'une d'elle est redondante
et, on obtient une solution en fonction de l'un des angles. Comme par
exemple: α
= 25° + β'. Idée (intuition ?) Pour
s'en sortir, il faut trouver une construction facilitatrice. Mais laquelle ? On
peut penser à un triangle symétrique du triangle bleu par rapport à DF. Une
sorte de rotation du triangle bleu autour de DF. Pour
cela, construisons le triangle rectangle ADG avec un angle de 20° en D, ce
qui conduit à 70° en G. Alors: Les
triangles rectangles ADG et CDE, avec AD = DC et les angles en D = 20°, sont
isométriques. Notamment DG = DE. Valeur de l'angle alpha Comparons
les deux triangles DFE (bleu) et DFG: Conclusion
les angles en F sont égaux et: α = 65° |
Figure initiale
Figure avec notations
Figure avec construction pour la solution
|
|
|
|
||
|
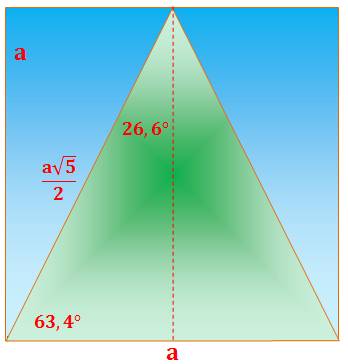
Ce triangle dans le carré est certainement isocèle, mais pas équilatéral. Longeur des côtés
Aire du triangle Angle à la base du triangle isocèle |
|
|
|
|
||
|
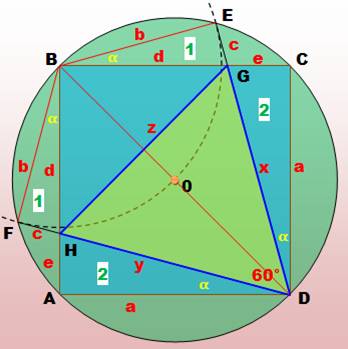
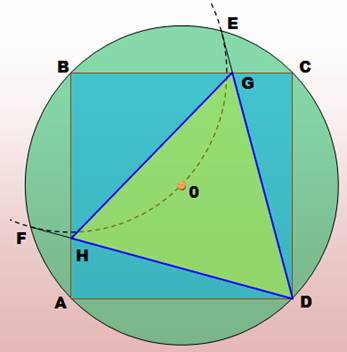
Comment inscrire un triangle équilatéral dans un carré? Les
sommets du triangle doivent se trouver sur les sommets ou les côtés du carré. Méthode d’abul-Wafa Un carré et son cercle circonscrit (centre O et rayon OA). Cercle de centre B de même rayon (pointillés). Il coupe le cercle circonscrit en E et F Les segments DE et DF coupent le carré en G et H. Le triangle DGH est un triangle équilatéral inscrit dans le
carré. |
|
|
|
Démonstration rapide Les triangles notés 2 sont égaux par symétrie due à
la construction. Ce qui conduit à : DG = DH. Le même raisonnement conduirait à l’égalité avec HG. Les trois côtés du triangle DGH sont égaux, c’est un
triangle équilatéral. Démonstration égalité des triangles notés 2 |
|
|
|
Les angles en A et C du carré sont droits: |
|
|
|
Les côtés du carré sont égaux: |
CD = DA |
|
|
Du fait de la symétrie de la constrution les arcs: |
EC et FA
sont égaux Et les angles
les interceptant aussi :
|
|
|
Avec ces trois éléments égaux deux à deux: |
Les
triangles noté 2 sont égaux (isométriques). |
|
|
Périmètre
du rectangle: PR = 2 x (100 + 96) = 392 La
somme des périmètres des trois triangles roses vaut: P3 = 300 +
288 + 84 = 672. Elle
représente une fois le périmètre du rectangle auquel on ajoute le périmètre
du triangle bleu PTB . P3 = PR + PTB PTB = P3 – PR
= 672 – 392 = 280 Remarque Le
quadrillage montre que les valeurs ne sont pas choisies au hasard. Les
longueurs des côtés du triangle bleu sont des nombres entiers. Ce qui
implique que les triangles roses sont des triangles
de Pythagore: 100² + 75² = 125²; 96² + 72² = 120²; 28² + 21² = 35² Une alternative avec a = 100 100² + 75² = 125²; 96² + 28² = 100²; 72² + 21² = 75² Toutes les solutions pour EG en dizaines et les autres
mesures jusqu'à 100: Il y
en a 21 pour 122 au total pour tous les EG de 1 à 100. |
|
|
10 /
(aucune) 20, 48, 52, 60, 11, 61, 9, 12, 15 30, 16, 34, 28, 21, 35, 9, 12, 15 30, 16, 34, 36, 15, 39, 15, 20, 25 30 / 40, 9, 41, 24, 32, 40, 8, 15, 17 50 / 60, 11, 61, 20, 48, 52, 12, 9, 15 60, 32, 68, 52, 39, 65, 21, 20, 29 60, 32, 68, 56, 42, 70, 18, 24, 30 60, 32, 68, 72, 30, 78, 30, 40, 50 60, 32, 68, 77, 36, 85, 24, 45, 51 60, 45, 75, 77, 36, 85, 24, 32, 40 |
70, 24, 74, 96, 40, 104, 30, 72, 78 80, 18, 82, 33, 44, 55, 36, 15, 39 80, 18, 82, 39, 52, 65, 28, 21, 35 80, 18, 82, 48, 64, 80, 16, 30, 34 80, 39, 89, 54, 72, 90, 8, 15, 17 80, 60, 100, 84, 35, 91, 45, 24, 51 90, 48, 102, 84, 13, 85, 77, 36, 85 90, 48, 102, 84, 63, 105, 27, 36, 45 90, 56, 106, 88, 66, 110, 24, 32, 40 100, 75, 125, 96, 28, 100, 72, 21, 75 100, 75, 125, 96, 72, 120, 28, 21, 35 |
Retour
/ Autres énigmes / Brève
482
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()