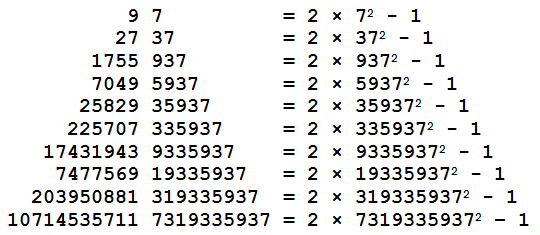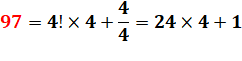0 NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/11/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Général	DicoNombre NOMBRES				Glossaire Général
96 95 / 94 93 / 92 / 91 / 90 85 / 80 70 60 50 40 30 20 10	97				98 99 100 101 à 120 500 1000 1 million
Nombre 97	Maths	Culture	Table de mul. en 90	Numération 90 à 99

CARTE D'IDENTITÉ
Nombre	Premier	Département	voir 971 et suite
Facteurs	97 = 1 x 97	Élément	BERKÉLIUM Bk
Ptés Typiques	/	Mnémo	PACK
	Suite Maths		Suite Culture

Propriétés CULTURELLES

Quatre-vingt-dix-sept

Quatre-vingt-dix-septième

Nonante sept

Nonante septième

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
noventa y siete novantasette	ninety-seven siebenundneunzig

Voir Numération 90 à 99

Nombres et langues

Économie

97 – L'identifiant international du compte bancaire (IBAN) obéit à l'arithmétique mod 97 pour la vérification des erreurs.

>>>

Propriétés MATHÉMATIQUES

Facteurs	97 = 1 x 97
Diviseurs	1, 97
Quantité	2
Somme	98
S - N	1

Auto-nombre

Déficient

Docile (amenable)

Emirp (97 et 79 sont premiers)

Heureux

Impair

Mian-Chowla

Narcissique de Keith

Premier (en 4n+1)

Premier bon

Premier de Pierpont

Premier de Pythagore

Premier de Woodall

Premier fort

Premier long

Premier permutable

Premier régulier

Premier résistant

Proth

Ulam

Voir Nom des nombres

16 – gonal centré

Voir Nombres géométriques

Chiffres et numération

Aucun nombre ajouté à ses chiffres ne donne 97			Auto-nombre.
9 + 7 = 16 = 4²	Curiosité (faible!): la somme des chiffres est un carré.
97 => 79 = 9 x 7 + 9 + 7	Son retourné est égal à la somme des chiffres augmenté du produit.
97	N'est repdigit dans aucune base. Il n'est pas brésilien.
97 – 9 – 7 = 81 = 3^4 = 9²	Devient carré ou bicarré en lui retirant ses chiffres.
97 = 7+3+7+4+2+4+1+2+6+8+9+4+9+2+8+2+6+0+4+9 97^10 = 73 742 412 689 492 826 049		Narcissique de Keith Somme avec ses chiffres et ceux de ses puissances. Voir Table des nombres de Keith
9710 = 8112 = 1889 9710 = 7613 = 6715 9710 = 6113 = 1691 9710 = 5219 = 2546 9710 = 4124 = 1493 9710 = 3132 = 1394 9710 = 2148 = 1295	Mêmes chiffres dans deux bases différentes, Sept fois. Plus petit cas.
97, 118, 85, 9 232 Cycle: 97, 292, 146, 73, 220, 110, 55, 166, 83, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, …	Le cycle de Syracuse de 97 comporte 118 étapes, un record. Il atteint une altitude maximale avec 9 232 au rang 85.
97 = 100 – 3	1/97 = 0,01 03 09 27 8 350.... Débute par les puissances de 3. Période de longueur 96.
97 = 9 + 7 + 5 + …+ 9 & 975 979 998 889 = 987 917²	Somme maximale des chiffres d'un carré inférieur à un million.

Addition et soustraction

97 = 29 + 31 + 37 = 22 + 24 + 25 + 26

Somme de premiers consécutifs. Aussi somme de composés consécutifs.

Multiplication, division, diviseurs

97 = 1 x 97 79 est aussi premier 89 est le premier précédent		Le plus grand premier < 100. Nombre premier circulaire ou permutable. Plus grand écart entre premier (97 – 89 = 8) pour la centaine de 2 à 100.
[2, 5], [4, 11], [6, 29], [8, 97],		Plus petits nombres premiers avec écart croissant par rapport au premier précédent.
97 = 2 x 7² – 1		Nombre premier de Woodall d'ordre 7.
97 x 1 = 97 97 x 2 = 194 97 x 3 = 291		Plus petit nombre de cette forme (3 premiers multiples avec un 9).
97, 907, 9007, 90007 et 900007		Nombres premiers en 9…7.
97 508 1596 4910 12 870 …	Quantité de nombres premiers à exactement trois chiffres distincts. Liste: 103, 107, 109, 127, 137, 139, 149, 157, 163, 167, 173, 179, 193, 197, 239, 241, 251, 257, 263, 269, 271, 281, 283, 293, 307, 317, 347, 349, 359, 367, 379, 389, 397, 401, 409, 419, 421, 431, 439, 457, 461, 463, 467, 479, 487, 491, 503, 509, 521, 523, 541, 547, 563, 569, 571, 587, 593, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 673, 683, 691, 701, 709, 719, 739, 743, 751, 761, 769, 809, 821, 823, 827, 829, 839, 853, 857, 859, 863, 907, 937, 941, 947, 953, 967, 971, 983. Il y a 508 nombres premiers avec 3 chiffres distincts de 1000 à 10 000. Liste: [1009, 1013, 1019, 1021, 1031 ... 9923, 9931, 9941, 9967, 9973] Il y a 1596 nombres premiers avec 3 chiffres distincts de 10 000 à 100 000. Liste : [10007, 10009, 10061, 10091, 10099 ... 99901, 99907, 99923, 99961, 99971] Etc.

Avec les puissances

97 = 4² + 9² 97 = 4 × 24 + 1			Nombre premier de Pythagore. Nombre premier de la forme 4n + 1. De tels nombres sont la somme une seule fois de deux carrés.
97 = 4² + 9² = 5² + 6² + 6² = 2^3 + 2^3 + 3^3 + 3^3 + 3^3 = 2^4 + 3^4 = 1^5 + 2^5 + 2^5 + 2^5				Seules sommes de carrés à deux ou trois termes >>> Somme de puissances dont cubes. Nombre binomial.
97 = 4² + 1x9² = 5² + 2x6² = 7² + 3x4² = 9² + 4x2²	= 1² + 6x4² = 5² + 8x3² = 4² + 9x3²				Nombre multi-somme de type A² + kB². Record après 73 avec sept représentations jusqu'à k = 10.
97 = 49² – 48² = 49 + 48				Motif valable pour tout nombre impair.
97 = 2^4 + 3^4		Somme des puissances 4 de deux premiers consécutifs. Le plus grand premier connu en tant que somme de la même puissance de deux premiers consécutifs (Gupta, cité par Prime Curios!)
97² = 65² + 72² = 4225 + 5184 = 9409				16^e triplet de Pythagore primitif.
97^2 = 9409 997² = 994009				Motif itératif sans fin.

En puissance

2^97 = 158 456 325 028 528 675 187 087 900 672 => 11 222 234 555 556 667 777 888 889	Le nombre obtenu en triant les chiffres par ordre croissant de cette puissance de 2 est premier.
97 = 2 × 7² – 1	Propriété qui se répète en ajoutant des chiffres à gauche. Voir ci-dessous.

Curiosité

Suite d'égalités trouvée par J.A.H. Hunter

On peut prolonger avec:

119565594194 77319335937 = 2 × 77319335937² – 1

1539378434417 877319335937 = 2 × 877319335937² – 1

Cette suite a une fin. En notant le nouveau chiffre à chaque itération, on a :

7, 3, 9, 5, 3, 3, 9, 1, 3, 7, 7, 8, 9, 8, 3, 4, 8, 3, 8, 8.

Voir Pépites

Dénombrement, jeux et curiosités

		Jeu du quatre 4.
97	Plus petit indice de la suite 4-Gödel à être non-entier.

Autour du nombre

13 135791113151719 13579111315 … 2931 135 79111315 … 6567 135 79111315 … 9597	Ces nombres, concaténations des nombres impairs successifs, sont premiers. Le nombre en …97 est le plus grand que je connaisse.
1/ 97 = 0,01 03 09 27 835 …		Suite des puissances de 3. Du fait que 97 = 100 – 3
Nombre premier long. La période du développement décimal de la fraction est maximale (96) en une seule suite permutée pour toutes les fractions avec ce dénominateur. Comment la période évolue selon le numérateur de k/97
			Bonne approximation de racine de 3. à 92 10 ^-6 près.
			Approximation de Pi avec 8 décimales donnée par Ramanujan

Factorielle 97 est "totalement première"

	Le nombre (97!) contient tous les nombres premiers jusqu'à 100. Le nombre 97! et la plus petite factorielle contenant textuellement tous les premiers inférieurs à lui. Seul dans ce cas au moins jusqu'à 1000!
Exemples 95! → 8 premiers manquants : [13, 19, 43, 61, 67, 79, 83, 89] 96! → 9 premiers manquants : [13, 17, 19, 23, 29, 31, 53, 59, 61] 98! → 5 premiers manquants : [13, 17, 31, 53, 71] 97! → 0 premier manquant 99! → 6 premiers manquants : [13, 19, 31, 47, 73, 83] 100! → 6 premiers manquants : [13, 19, 31, 47, 73, 83] … 500! → 23 premiers manquants : [109, 113, 131, 137, 139, 157, 167, 179, 181, 191, 197, 211, 223, 227, 239, 257, 293, 307, 311, 347, 419, 431, 499]
Programme Python from sympy import primerange def BON(max_n: int) -> list[int]: # 1) Liste de tous les premiers jusqu'à max_n primes = list(primerange(2, max_n + 1)) complets = [] fact = 1 for n in range(2, max_n + 1): fact *= n s = str(fact) if all(str(p) in s for p in primes if p <= n): complets.append(n) return complets if __name__ == "__main__": bons_n = BON(500) print("BON pour: ", bons_n) Résultat BON pour: [2, 97]

Voir Programmation – Index / Programmes Python – Index / Brève 53/1249

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 0, 0, 0, 1] 3, [1, 0, 1, 2, 1] 4, [1, 2, 0, 1] 5, [3, 4, 2] 6, [2, 4, 1] 7, [1, 6, 6] 8, [1, 4, 1] 9, [1, 1, 7] 10, [9, 7] 11, [8, 9]	12, [8, 1] 13, [7, 6] 14, [6, 13] 15, [6, 7] 16, [6, 1] 17, [5, 12] 18, [5, 7] 19, [5, 2] 20, [4, 17] 21, [4, 13]	22, [4, 9] 23, [4, 5] 24, [4, 1] 25, [3, 22] 26, [3, 19] 27, [3, 16] 28, [3, 13] 29, [3, 10] 30, [3, 7] 60, [1, 37]	96, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 98 Voir en haut de page DicoNombre
Site	97 – Prime Curios!
Cette page	http://diconombre.fr/NombDico/Nb50a100/Nb97.htm