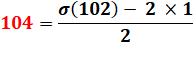|
Édition du: 06/03/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 60
/ 70
/ 75 / 76
/ 77 / 78
/ 79 / 80
/ 81 / 82
/ 83 / 84
/ 85 / 86
/ 87 / 88
/ 89 / 90
/ 91 / 92
/ 93 / 94
/ 95 / 96
/ 97 / 98
/ 99 / 100 / 101 / 102 / 103
|
104 |
105 / 106 / 107
/ 108 / 109 / 110 / 111 / 112
/ 113 / 114 / 115 / 120 / 130 / 140
/ 150 / 200 / 250 / 300 / 400
/ 500 / 1000
/ Autres |
|
![]()
|
|
|
|||
|
Suite en propriétés
arithmétiques |
|
|
||
Le plus petit nombre composé tel que la
somme de ses diviseurs plus 6 = la somme des diviseurs du nombre plus 6. |
||||
|
|
||
|
|
|
104
+ 401 = 505 |
|
Addition et soustraction
|
104
= 6 + 8 + 10 +
12 + 14 + 16 + 18 + 20 |
|
|
104
= 2 + 3 + … + 14 |
|
|
104
= 1 + 4 + 8 + 13
+ 26 + 52 |
|
|
104
= 52 + 26 + 13 + 8 + 4 + 1 |
|
Multiplication, division, diviseurs
|
104 =
8 x 13 |
|
|
|
104 =
(25² – 1) / 6 104 |
(25² – 1) |
|
|
|
104 = 23 x 13 => 2 + 13 =
15 105 = 3 x 5 x 7 => 3 + 5 + 7 = 15 |
|
|
|
104 =
13 × 8 |
|
|
|
|
|
|
|
|
Liste: 20, 104,
464, 650, 1952, … |
|
|
|
|
|
![]()
Avec les puissances
|
104 = 2² + 10² = (1² + 1²) (4² + 6²) = (2² + 2²) (2² +
3²) = 2² + 6² + 8² = 4² + 4² + 6² + 6² |
|
Dénombrement,
jeux et curiosités
|
|
|
|
|
Le
pentagone + étoile répond au problème, mais les segments se croisent. La
longueur des segments est quelconque. |
|
104
= 16(16 – 3) / 2 |
|
|
104, 105, 106 6200, 6201, 6202 |
|
Autour du nombre
|
11104 + 1 = k ×
118 + 1 =
2,017… 10108 = 201761945
2673378577 6567657453 6564372041 2860730997 6318704769 7577841101 1384530553
3669808023 7620229028 5695900642 k
= p41 * p60 = 8 6759222313
4283908122 1807709585 0708048977 × 1084881048 5363747061 2961399842
9729484098 3461152579 0577216753 |
|
Décimales
|
|
|
|
|
![]()
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
104 2,
[1, 1, 0, 1, 0, 0, 0] 3,
[1, 0, 2, 1, 2] 4,
[1, 2, 2, 0] 5, [4, 0, 4] 6, [2, 5, 2] 7,
[2, 0, 6] 8,
[1, 5, 0] 9,
[1, 2, 5] 10,
[1, 0, 4] 11,
[9, 5] |
12, [8, 8] 13,
[8, 0] 14, [7, 6] 15,
[6, 14] 16,
[6, 8] 17,
[6, 2] 18,
[5, 14] 19,
[5, 9] 20,
[5, 4] 21,
[4, 20] |
22,
[4, 16] 23,
[4, 12] 24,
[4, 8] 25, [4, 4] 26,
[4, 0] 27,
[3, 23] 28,
[3, 20] 29,
[3, 17] 30,
[3, 14] 60,
[1, 44] |
12,
[8, 8] 25,
[4, 4] 51,
[2, 2] 103,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()